SOLVING SYSTEMS OF INEQUALITIES WITH ONE VARIABLE

Example 1 :

Solve the following system of linear inequalities 

3x - 6 ≥ 0,  4x - 10 ≤ 6

Solution :

Solving the equations separately

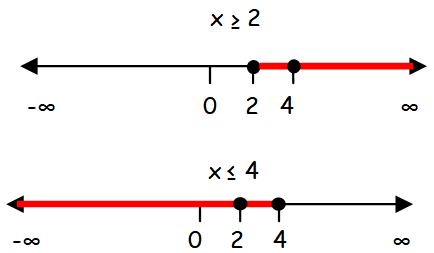
The solution set of first given inequality is [2,  ∞).

The solution set of second given inequality is (-∞, 4]

The intersection of these solution sets is the set [2, 4].

Example 2 :

Solve the following system of linear inequalities 

(5x/4) + (3x/8)  >  39/8

(2x - 1)/12 - (x - 1)/3 < (3x + 1)/4

Solution :

Solving the first given inequality 

(5x/4) + (3x/8)  >  39/8

(10x + 3x)/8 > 39/8

(13x/8)  > 39/8

Multiplying by 8 through out the equations

13x > 39

Divide by 13, we get

x > 39/13

x > 3

Solution set of the first given inequality is (3, ∞)

Solving the second given inequality :

(2x - 1)/12 - (x - 1)/3 < (3x + 1)/4

[(2x - 1) - 4(x - 1)]/12 < (3x + 1)/4

[(2x - 1 - 4x + 4)]/12 < (3x + 1)/4

(-2x + 3)/12 < (3x + 1)/4

Multiply 12 on both sides

(-2x + 3) < 3(3x + 1)

-2x + 3 < 9x + 3

Subtract 9x on both sides

-2x - 9x + 3 < 3

Subtract 3 on both sides

-11x  < 0

Divide by -1 on both sides

x > 0

The solution set of the second inequality is (0, ∞)

The intersection of the two solutions sets is (3, ∞).

So, the solution of given inequalities is (3, ∞).

Example 3 :

A circuit overloads at 1800 watts of electricity. You plug a microwave oven that uses 1100 watts of electricity into the circuit.

a. Write and solve an inequality that represents how many watts you can add to the circuit without overloading the circuit.

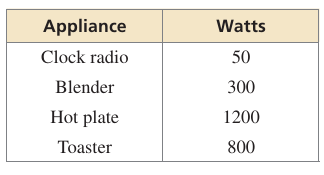
b. In addition to the microwave oven, which of the following appliances can you plug into the circuit at the same time without overloading the circuit

Solution :

You know that the microwave oven uses 1100 watts out of a possible 1800 watts.

Let w be the additional watts you can add to the circuit.

1100 + w < 1800

Solving for w, we get

w < 1800 - 1100

w < 700

b)  You can add up to 700 watts to the circuit, which means that you can also plug in the clock radio and the blender.

Look Back You can check that your answer is correct by adding the numbers of watts used by the microwave oven, clock radio, and blender.

1100 + 50 + 300 = 1450

The circuit will not overload because the total wattage is less than 1800 watts.

You start a small baking business, and you want to earn a profit of at least $250 in the first month. The expenses in the first month are $155. What are the possible revenues that you need to earn to meet the profit goal?

Example 4 :

You save $15 per week to purchase one of the bikes shown.

a. Write and solve an inequality to find the number of weeks you need to save to purchase a bike. 

b. Your parents give you $65 to help you buy the new bike. How does this affect your answer in part (a)? Use an inequality to justify your answer.

Solution :

a)  Let x be the number of weeks you need to save to purchase the bike.

Starting price of the bike = $120

So, the amount what we should as savings will be greater than 120.

15x > 120

x > 120/15

x > 8

So, the minimum number of weeks required to make the saving is 8.

b) Amount given by parent = $65

65 + 15x > 120

15x > 120 - 65

15x > 55

x > 55/15

x > 3.6

Approximately 4 weeks.

Example 5 :

A state imposes a sales tax on items of clothing that cost more than $175. The tax applies only to the difference of the price of the item and $175.

a. Use the receipt shown to find the tax rate (as a percent).

b. A shopper has $430 to spend on a winter coat. Write and solve an inequality to find the prices p of coats that the shopper can afford. Assume that p ≥ 175.

c. Another state imposes a 5% sales tax on the entire price of an item of clothing. For which prices would paying the 5% tax be cheaper than paying the tax described above? Write and solve an inequality to find your answer and list three prices that are solutions.

Solution :

a) Sales tax = Difference between the original price and 175

= 295 - 175

r of (295 - 175) = 7.5

(r) 120 = 7.5

r = 7.5/120

r = 0.0625

Converting as percentage 0.0625 x 100%

= 6.25%

So, the tax rate is 6.25%.

b)  p + 6.25% of (p - 175) ≤ 430

p + 0.0625(p - 175) ≤ 430

p + 0.0625p - 10.93 ≤ 430

1.0625p - 10.93 ≤ 430

1.0625p ≤ 430 + 10.93

1.0625p ≤ 440.93

p ≤ 440.93/1.0625

p ≤ 414.9

approximately p ≤ 415

So, the value of p is 175 < p ≤ 415

c)  5% of p < 6.25% of (p - 175)

0.05p < 0.0625(p - 175)

0.05p < 0.0625p - 10.93

0.05p - 0.0625p < -10.93

-0.0125p < -10.93

p > 10.93/0.0125

p > 874.4

approximately p > 875

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.