SOLVING TWO-STEP AND MULTI-STEP INEQUALITIES

Inequalities that contain more than one operation require more than one step to solve. Use inverse operations to undo the operations in the inequality one at a time.

Solving Two-Step Inequalities

Solve each inequality and graph the solutions : 

Example 1 : 

170 + 4x ≤ 510

Solution :

170 + 4x ≤ 510

Because 170 is added to 4x, subtract 160 from each side to undo the addition.

(170 + 4x) - 170 ≤ 510 - 170

170 + 4x - 170 ≤ 340

4x ≤ 340

Because x is multiplied by 4, divide each side by 4 to undo the multiplication.

4x/4 ≤ 340/4

x ≤ 85

Example 2 : 

8 - 2y ≤ 22

Solution :

8 - 2y ≤ 22

Because 8 is added to -2y, subtract 8 from each side to undo the addition.

(8 - 2y) - 8 ≤ 22 - 8

8 - 2y - 8 ≤ 14

-2y ≤ 14

Because y is multiplied by -2, divide each side by -2 to undo the multiplication and change ≤ to ≥.

-2y/(-2) ≥ 14/(-2)

y ≥ -7

Solving Multi-Step Inequalities

Solve each inequality and graph the solutions : 

Example 3 : 

(7x + 2)/5 < 8.8

Solution :

(7x + 2)/5 < 8.8

Because (7x + 2) is divided by 5, multiply each side by 5 to undo the division.

5[(7x + 2)/5] < 5(8.8)

7x + 2 < 44

Because 2 is added to 7x, subtract 2 from each side to undo the addition.

(7x + 2) - 2 < 44 - 2

7x + 2 - 2 < 44 - 2

7x < 42

Because x is multiplied by 7, divide each side by 7 to undo the multiplication.

7x/7 < 42/7

x < 6

x < 6

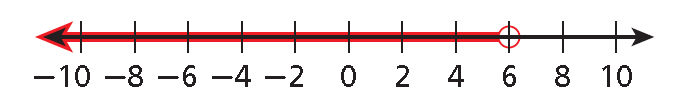
Example 4 : 

(1 -3y)/2 ≤ -2.5  

Solution :

(1 -3y)/2 ≤ -2.5  

Because (1 - 3y) is divided by 2, multiply each side by 2 to undo the division.

2[(1 - 3y)/2] ≤ 2(-2.5)

1 - 3y ≤ -5

Because 1 is added to -3y, subtract 1 from each side to undo the addition.

(1 -3y) - 1 ≤ -5 - 1

1 - 3y - 1 ≤ -6

-3y ≤ -6

Because y is multiplied by -3, divide each side by -3 and change ≤ to ≥.

-3y/(-3) ≥ -6/(-3)

y ≥ 2

Simplifying Before Solving Inequalities

Solve each inequality and graph the solutions : 

Example 5 : 

-5 + (-7) < -5x - 2

Solution :

-5 + (-7) < -5x - 2

Combine like terms. 

-12 < -5x - 2

Because 2 is subtracted from -5x, add 2 to each side to undo the subtraction.

-12 + 2 < (-5x - 2) + 2

-10 < -5x - 2 + 2

-10 < -5x

Because x is multiplied by -5, divide each side by -5 to undo the multiplication and change < to >.

-10/(-5) > -5x/(-5)

2 > x

x < 2

Example 6 : 

-3(3 - y) < 16

Solution :

-3(3 - y) < 16

Distribute -3 on the left side.

-9 + 3y < 16

Because -9 is added to 3y, add 9 to each side to undo the addition.

9 + (-9 + 3y) < 9 + 16

9 - 9 + 3y < 25

3y < 25

Because y is multiplied by 3, divide each side by 3 to undo the multiplication.

3y/3 < 25/3

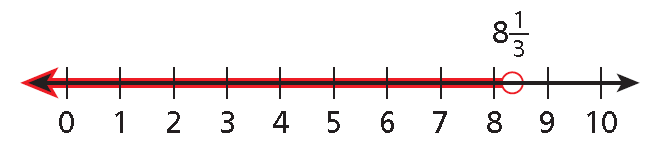
y < 8⅓

Example 7 : 

4m/5 + 1/2 < 3/5

Solution :

4m/5 + 1/2 < 3/5

In the fractions above, we find the denominators 2 and 5. 

Least common multiple of the denominators (2, 5) = 10.

Multiply each side by the least common multiple, 10 to get rid of the fractions. 

10(4m/5 + 1/2) < 10(3/5)

10(4m/5) + 10(1/2) < 30/5

40m/5 + 10/2 < 6

8m + 5 < 6

Because 5 is added to 8m, subtract 5 to each side to undo the addition.

(8m + 5) - 5 < 6 - 5

8m + 5 - 5 < 1

8m < 1

Because x is multiplied by 8, divide each side by 8 to undo the multiplication.

8m/8 < 1/8

m < 1/8

Gardening Application

Example 8 : 

To win the blue ribbon for the Heaviest Pumpkin Crop at the county fair, the average weight of David's two pumpkins must be greater than 829 lb. One of his pumpkins weighs 897 lb. What is the least number  of pounds the second pumpkin could weigh in order for David to win the blue ribbon?

Solution :

Let y represent the weight of the second pumpkin. The average weight of the pumpkins is the sum of each weight divided by 2.

(897 plus y) divided by 2 must be greater than 829

(897 + y)/2 > 829

Because (897 + y) is divided by 2, multiply each side by 2 to undo the division.

2[(897 + y)/2] > 2(829)

897 + y > 1658

Because 897 is added to y, subtract 897 from each side to undo the addition.

(897 + y) - 897 > 1658 - 897

897 + y - 897 > 761

y > 761

The second pumpkin must weigh more than 761 pounds.

Check :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.