STANDARD DEVIATION FOR CONTINUOUS DATA
Mean Method :
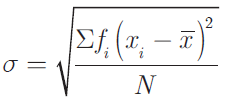
where xi = Middle value of the ith class.
fi = Frequency of the ith class
Step Deviation Method :
To make the calculation simple, we provide the following formula. Let A be the assumed mean, xi be the middle value of the ith class and c is the width of the class interval.
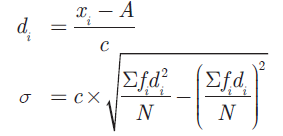
Example 1 :
The measurements of the diameters (in cms) of the plates prepared in a factory are given below. Find its standard deviation.
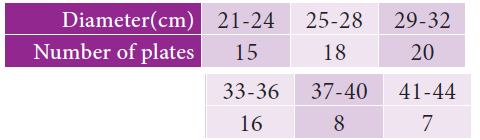
Solution :
|
20.5 - 24.5 15 |
24.5 - 28.5 18 |
28.5 - 32.5 20 |
|
32.5 - 36.5 16 |
36.5 - 40.5 8 |
40.5 - 44.5 7 |
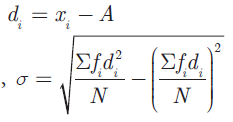
x is the mid value of the given set.
d = (x - 34.5)/2
|
x 22.5 26.5 30.5 34.5 38.5 42.5 |
d -6 -4 -2 0 2 4 |
f 15 18 20 16 8 7 |
d2 36 16 4 0 4 16 |
fd2 540 288 80 0 32 112 |
fd -90 -72 -40 0 16 28 |
Σf = N = 84
Σfd2 = 1052
(Σfd2/N) = (1052/84) = 263/21
Σfd = -158
(Σfd/N)2 = (-158/84)2 = (79/42)2
σ = √(22092-6241)/1764
σ = (√15851/1764) ⋅ 2
σ = √8.98 ⋅ 2
σ = 2.99 ⋅ 2
σ = 5.99
Hence the required standard deviation is 6.
Example 2 :
The time taken by 50 students to complete a 100 meter race are given below. Find its standard deviation
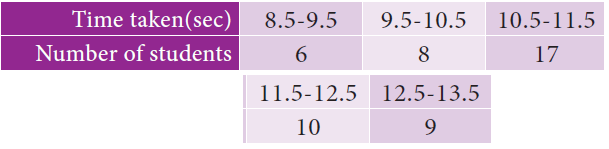
Solution :
x is the mid value of the given set.
d = (x - 22)/2
|
x 18 20 22 24 26 |
d -2 -1 0 1 2 |
f 6 8 17 10 9 |
d2 4 1 0 1 4 |
fd2 24 8 0 10 36 |
fd -12 -8 0 10 18 |
Σf = N = 50
Σfd2 = 78
(Σfd2/N) = (78/50) = 39/25
Σfd = 8
(Σfd/N)2 = (8/50)2 = (4/25)2 = 16/625
σ = √(975 - 16)/625
σ = √959/625
σ = (√1.533) ⋅ 2
σ = 1.23 ⋅ 2
σ = 2.47
Hence the required standard deviation is 2.47.
Example 3 :
Calculate the standard deviation and variance of the following data given below.
|
Class interval 4-8 8-12 12-16 16-20 |
Frequency 3 6 4 7 |
Solution :
Since we have less number of data values, we have may use the direct method to find the standard deviation and variance.
But the data values are as class intervals, we have to find the mid value to fix x.
|
Class interval 4-8 8-12 12-16 16-20 |
Mid value 6 10 14 18 |
Frequency 3 6 4 7 |
Mean = [6(3) + 10(6) + 14(4) + 18(7)] / (3 + 6 + 4 + 7)
= (18 + 60 + 56 + 126) / 20
= 260/20
= 13
|
x 6 10 14 18 |
x - 13 -7 -3 1 5 |
f 3 6 4 7 |
(x-X̅)2 49 9 1 25 |
f(x-X̅)2 147 54 4 175 |
Σf(x-X̅)2 = 147 + 54 + 4 + 175
= 380
Σf = 20
Calculating standard deviation :
Variance :
σ = √19
σ2 = 19
Variance = 19
Example 4 :
Calculate the mean, standard deviation and variance of the following data given below.
|
Classes 1 - 10 10 - 20 20 - 30 30 - 40 40 - 50 50 - 60 |
Frequency 11 29 18 4 5 3 |
Solution :
Finding the mid value.
Calculating mean :
= [5.5(11) + 15.5(29) + 25.5(18) + 35.5(4) + 45.5(5) + 55.5(3)] / 70
= (60.5 + 449.5 + 459 + 142 + 227.5 + 166.5) / 70
= 1505/70
= 21.5
So, the mean is 21.5
|
x 5.5 15.5 25.5 35.5 45.5 55.5 |
d=x-25.5 -20 -10 0 10 20 30 |
d2 400 100 0 100 400 900 |
f 11 29 18 4 5 3 |
fd -220 -290 0 40 100 90 |
fd2 4400 2900 0 400 2000 2700 |
Σfd = -220 + (-290) + 0 + 40 + 100 + 90
= -510 + 230
= -280
Σfd2 = 4400 + 2900 + 0 + 400 + 2000 + 2700
= 12400
Σf = 11 + 29 + 18 + 4 + 5 + 3
= 70
Approximately the standard deviation is 12.7
Variance = 161.14 approximately 161.
Example 5 :
Life of blubs produced by two factories A and B are given below.
|
Length of life (in hours) 550 - 650 650 - 750 750 - 850 850 - 950 950 - 1050 |
Factory A 10 22 52 20 16 ---- 120 |
Factory B 8 60 24 16 12 ---- 120 |
The bulb of which factory are more consistent from the point view length of life ?
Solution :
Class length = 100, let us find mid value to fix x.
|
x 600 700 800 900 1000 |
d=(x - 800)/100 -2 -1 0 1 2 |
f(for A) 10 22 52 20 16 |
f(for B) 8 60 24 16 12 |
For Bulb A :
Σfd = 10(-2) + 22(-1) + 52(0) + 20(1) + 16(2)
= -20 - 22 + 0 + 20 + 32
= -42 + 52
= 10
Σfd2 = 10(-2)2 + 22(-1)2 + 52(0)2 + 20(1)2 + 16(2)2
= 40 + 22 + 0 + 20 + 64
= 146
Σf = 120
For Bulb B :
Σfd = 8(-2) + 60(-1) + 24(0) + 16(1) + 12(2)
= -16 - 60 + 0 + 16 + 24
= -76 + 40
= -36
Σfd2 = 8(-2)2 + 60(-1)2 + 24(0)2 + 16(1)2 + 12(2)2
= 32 + 60 + 0 + 16 + 48
= 156
Σf = 120
Standard deviation for bulb A :
Standard deviation for bulb B :
Factory A is more consistent.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Resources (Videos, Concepts, Worksheets and More)
Dec 23, 24 03:47 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 91)
Dec 23, 24 03:40 AM
Digital SAT Math Problems and Solutions (Part - 91) -
Digital SAT Math Problems and Solutions (Part - 90)
Dec 21, 24 02:19 AM
Digital SAT Math Problems and Solutions (Part - 90)