STRETCH A GRAPH VERTICAL HORIZONTAL EXAMPLES

About "Stretch a Graph Vertical or Horizontal Examples"

Stretch a Graph Vertical or Horizontal Examples :

Here we are going to learn how to stretch a graph vertically or horizontally.

Stretching a Graph Vertically or Horizontally - Examples

The procedure for stretching the graph of a function vertically or horizontally is illustrated by the following examples :

Question 1 :

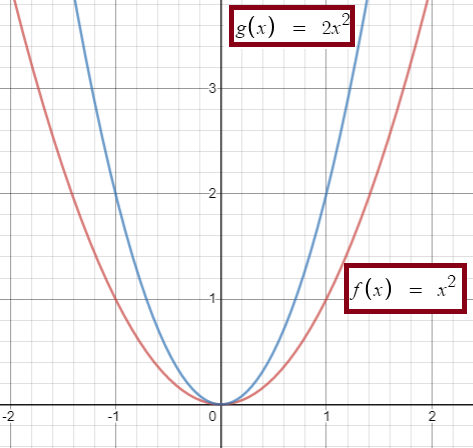
Define a function g by g(x)  =  2f(x),

where f is the function defined by f(x) = x², with the domain of f the interval [−1, 1].

(a) Find the domain of g.

(b) Find the range of g.

(c) Sketch the graph of g.

Solution :

(a)  Here the function g(x) is defined by the function f(x), so the domain of both functions will be same. Hence the domain of g in the interval [-1, 1].

(b)  By multiplying each range of f(x) by 2, we get the range of the function g(x). 

Range of f(x) by applying domain, we get

f(x) = x²

If x = -1, then y  = 1

If x = 0, then y  = 0

If x = 1, then y  = 1

Range of f(x) is [0, 1]. By multiplying 2, we get the range of g(x). That is [0, 2]. 

(c)  Since 2 is the integer multiplied with the function, we have to stretch the graph vertically.

Question 2 :

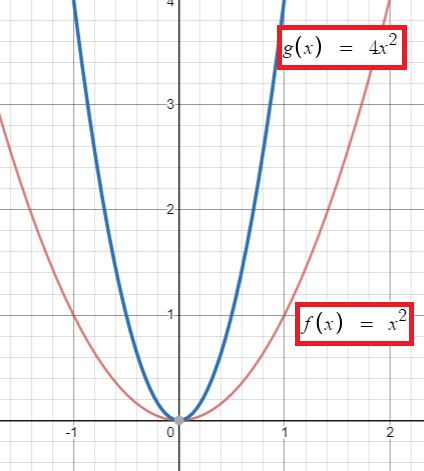
Define a function h by 

h(x) = f(2x),

where f is the function defined by f(x) = x², with the domain of f the interval [−1, 1].

(a) Find the domain of h.

(b) Find the range of h.

Solution :

(a)  The formula defining h shows that h(x) is defined precisely when f(2x) is defined, which means that 2x must be in the interval [−1, 1].

Here the constant c is 1/2, which means that x must be in the interval [−1/2 , 1/2 ]. Thus the domain of h is the interval [−1/2 , 1/2].

(b) Because h(x) equals f(2x), we see that the values taken on by h are the same as the values taken on by f . Thus the range of h equals the range of f , which is the interval [0, 1].

After having gone through the stuff given above, we hope that the students would have understood "Stretch a Graph Vertical or Horizontal Examples". 

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.