SUBSTITUTION METHOD EXAMPLES

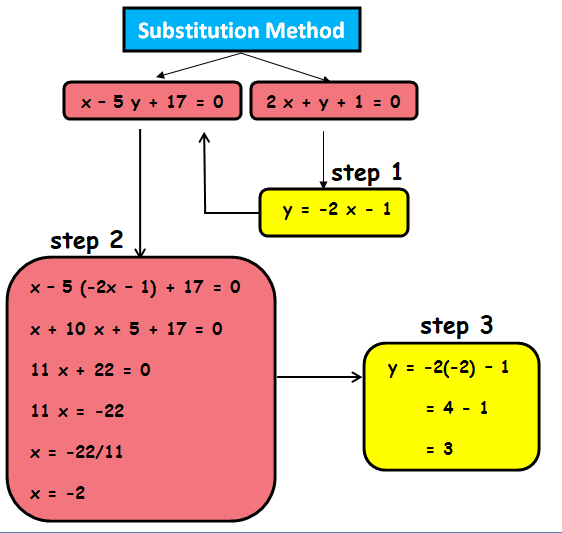
The following steps will be useful to solve the systems of linear equations using substitution.

Step 1 : 

In the given two equations, solve one of the equations either for x or y. 

Step 2 : 

Substitute the result of step 1 into other equation and solve for the second variable. 

Step 3 : 

Using the result of step 2 and step 1, solve for the first variable.  

Practice Questions

Question 1 :

Solve the following equations by substitution method.

5 x - 3 y - 8  =  0  and 2x - 3 y - 5  = 0  

Solution :

5 x - 3 y - 8 = 0  ------(1)

 2 x - 3 y - 5  = 0  ------(2)

So,

(x, y)  =  (-2, 3)

Question 2 :

Solve the following equations using substitution method.

5x - 3y - 8 = 0  and  2x - 3y - 5  = 0

Solution :

5x - 3y - 8 = 0  ------(1) 

2x - 3y - 5  = 0  ------(2) 

-3y  =  -5x + 8

3y  =  5x - 8

Apply the value of 3y in the second equation, we get

2x - (5x - 8)  - 5  =  0

2x - 5x + 8 - 5  =  0

-3x + 3  =  0

-3x  =  -3  ==>  x  =  -3/(-3)  ==> x  =  1

Substitute x  =  1 in the equation 3y  =  5x - 8, we get

3y  =  5(1) - 8

3y  =  5 - 8

3y  =  -3  ==>  y  =  (-3)/3  ==>  y  = -1

So, 

(x, y)  =  (1, -1)

Question 3 :

Solve the following equations by substitution method

y  =  6x - 11 and -2x - 3y  =  -7

Solution :

y  =  6x - 11 ------(1)

-2x - 3y  =  -7 ------(2)

Substitute the value of y in the second equation, we get

-2x - 3(6x - 11)  =  -7

-2x - 18x + 33  =  -7

-20x + 33  =  -7

Subtract 33 on both sides

-20x + 33 - 33  =  -7 - 33

-20x  =  -40

Divide by -20 on both sides

-20x/(-20)  =  -40/(-20)

x  =  2 

Substitute x  =  2 in the first equation, we get

y  =  6(2) - 11 

y  =  12 - 11 ==>  1

So,

(x, y)  =  (2, 1)

Question 4 :

Solve the following equations by substitution method 

2x − 3y = −1 and y = x − 1

Solution :

2x − 3y = −1 -----(1) 

y = x − 1  -----(2) 

Substitute y = x - 1 in the first equation

2x - 3(x - 1)  =  -1

2x - 3x + 3  =  -1

-x + 3  = -1

Subtract by 3 on bot sides,

-x + 3 - 3  =  -1 - 3

-x  =  -4  ==> x  =  4

Apply x  =  4 in the equation y  =  x - 1

y  =  4 - 1  ==>  y  =  3

So,

(x, y)  =  (4, 3)

Question 5 :

Solve the following equations by substitution method 

y = −3x + 5 and 5x − 4y = −3

Solution :

y = −3x + 5 -------(1)

5x − 4y = −3 -------(2)

Substitute y  =  -3x + 5 in the second equation

5x - 4 (-3x + 5)  =  -3

5x + 12x - 20  =  -3

17x  =  -3 + 20

17x  =  17

Divide by 17 on both sides

17x/17  =  17/17  ==> x  =  1 

Applying x  =  1 in the first equation, we get

y  =  -3(1) + 5

y  =  -3 + 5  ==>  y  =  2

So,

(x, y)  =  (1, 2)

Question 6 :

Solve the following equations by substitution method 

 −3x − 3y = 3 and  y = −5x − 17

Solution :

−3x − 3y = 3 -------(1) 

y = −5x − 17  -------(2)

Substitute y  =  -5x - 17 in the first equation

−3x − 3(-5x - 17) = 3

-3x + 15x + 51  =  3

12x + 51  =  3

Subtract by 51 on both sides

12x + 51 - 51  =  3 - 51

12x =  -48

Divide by 12 on both sides

12x/12  =  -48/12  ==>  x  =  -4 

Applying x  =  -4 in the second equation

y  =  -5(-4)  - 17

y  =  20 - 17

y  =  3

So,

(x, y)  =  (-4, 3)

Question 7 :

Solve the following equations by substitution method 

y = 5x − 7 and −3x − 2y = −12 

Solution :

y = 5x − 7  -------(1) 

−3x − 2y = −12  -------(2)

Substitute y  =  5x − 7 in the second equation

−3x − 2(5x - 7) = −12

−3x − 10x + 14 = −12

-13x + 14 =  -12

Subtract 14 on both sides

-13x + 14 - 14  =  -12 - 14

-13x  =  -26

Divide by -13 on both sides

-13x/(-13)  =  -26/(-13)

x  =  2

Apply x = 2 in the equation y  =  5x - 7

y = 5(2)  - 7

y  =  10 - 7 ==>  3

So,

(x, y)  =  (2, 3)

Question 8 :

Solve the following equations by substitution method 

−4x + y = 6 and −5x − y = 21

Solution :

−4x + y = 6  -------(1) 

−5x − y = 21  -------(2)

From the first equation,

y  =  6 + 4x

Substitute y  =  6 + 4x in the second equation

−5x − (6 + 4x) = 21

-5x - 6 - 4x  =  21

-9x - 6  =  21

Add 6 on both sides

-9x - 6 + 6  =  21 + 6

-9x  =  27

Divide by -9 on both sides

-9x/(-9)  =  27/(-9)

x  =  -3

Apply x = -3 in the equation y  =  6 + 4x

y = 6 + 4(-3)

y  =  6 - 12  =  -6

So,

(x, y)  =  (-3, -6)

Question 9 :

Solve the following equations by substitution method 

 2x + y = 20 and 6x − 5y = 12

Solution :

 2x + y = 20  -------(1) 

6x − 5y = 12  -------(2)

From the first equation, we get 

y  =  20 - 2x

Substitute y  =  20 - 2x in the second equation

6x − 5 (20 - 2x) = 12

6x - 100 + 10x  =  12

16x - 100  = 12

Add 100 on both sides

16x - 100 + 100  =  12 + 100

16x  =  112

Divide by 16 on both sides

16x/16  =  112/16

x  =  7

Apply x  =  7 in the equation y  =  20 - 2x 

y  =  20 - 2(7)

y  =  20 - 14  ==>  6

So,

(x, y)  =  (7, 6)

Question 10 :

Solve the following equations by substitution method 

y = −2 and 4x − 3y = 18 

Solution :

y = −2 -------(1) 

4x − 3y = 18  -------(2)

Apply y  =  -2 in the second equation

4x − 3(-2) = 18

4x + 6  =  18

Subtract by 6 on both sides

4x + 6 - 6  =  18 - 6

4x  =  12

Divide by 1 on both sides

4x/4  =  12/4

x  =  3

So,

(x, y)  =  (3, -2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.