SURFACE AREA OF 3D SHAPES

Surface area of 3d shapes :

Here, we are going to see, how to calculate surface area of 3-D shapes such as cubes, cuboids, prisms and pyramids.

The basic idea to find surface area of any 3-D shape is to add the areas of all faces. 

Surface area of cuboid

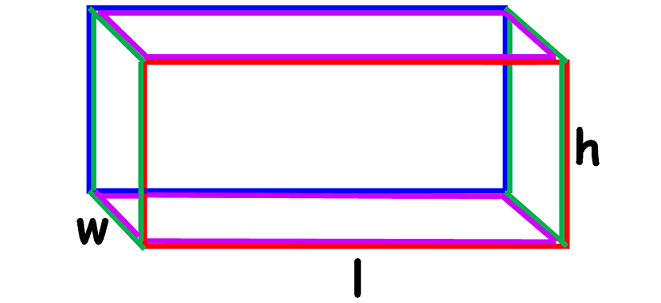
Based on the idea given above, the surface area of the above cuboid is given below. 

Surface Area  =  Sum of areas of all six faces

Let us find the area of each face separately. 

Area of the front face (red colored)  =  l x h

Area of the back face (blue colored)  =  l x h

Area of the left side face (green colored)  =  w x h

Area of the right side face (green colored)  =  w x h

Area of the top portion (purple colored)  =  l x w

Area of the base (purple colored)  =  l x w

Now, 

Surface area  =  lh + lh + wh + wh + lw + lw 

Surface area  =  2lh + 2wh + 2lw

Surface area of  =  2( lh + wh + lw )

This is the formula to find surface area of a cuboid. 

Surface area of cube

We can apply the above explained basic idea to find surface area of any prism without remembering the formulas. 

Let us find surface area of the cube given below. 

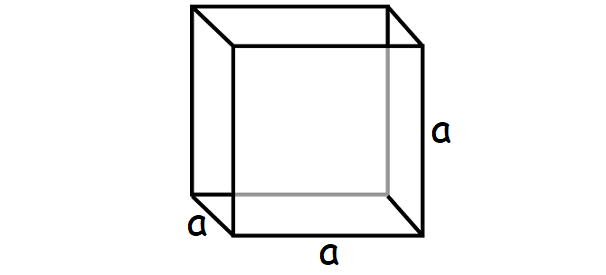
We know that the shape of each face of a cube is a square.

In the above cube, the side length of each face is "a". 

So, area of each face (square)  =  a x  a  =  a²

Therefore,

surface area of the cube  =  6 x area of each face 

Surface area of cube  =  6a²

Surface area of triangular prism

Now, let us find surface area of the triangular prism given below. 

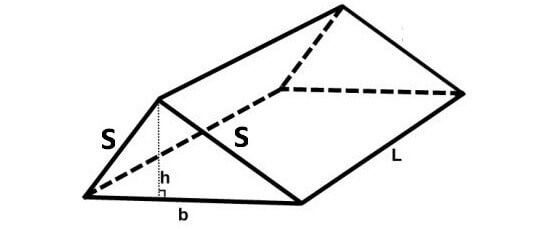
In the above triangular prism, there are five faces. The shape of the base and the two slanting faces is rectangle. The shape of two faces on the left side and right side  is triangle. 

For the given triangular prism, 

Area of the base  =  Lb 

Area of the first slanting face  =  Ls

Area of the other slanting face  =  Ls

Area of the front face  =  (1/2)bh

Area of the back face   =  (1/2)bh

So,

surface area  =  sum of the area of 5 faces

surface area  =  Lb + 2Ls +2x(1/2)bh

Surface area of triangular prism = Lb+2Ls+bh

Surface area of pyramids

Now, let us find surface area of the pyramid given below. 

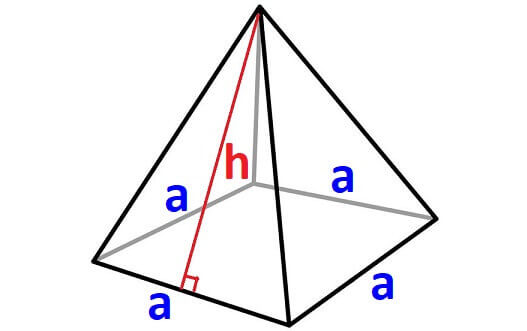
Surface Area  =  Sum of areas of all five faces (Including the base)

For any pyramid, if the shape of the base is square, then we will have four side walls. The shape of each side wall will be a triangle with equal area.  

In the above pyramid, the base is a square with side length "a" and each wall is a triangle with base "a" and height "h"

Let us find the area of each face separately. 

Area of the base  =  a x a  =  a²

Area of each side wall  =  (1/2)ah 

Area of all four side walls  =  4 x (1/2)ah  =  2ah 

Surface area of the above pyramid  =  a² + 2ah 

This is the formula to find surface area of a pyramid with square base. 

We can apply the above explained basic idea to find surface area of a pyramid with triangular base. 

Let us find surface area of a pyramid with triangular base

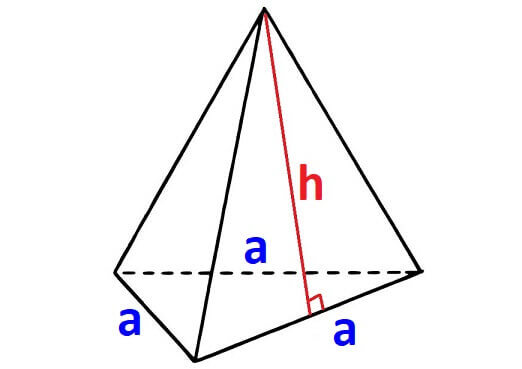
For any pyramid, if the shape of the base is equilateral  triangle, then we will have three side walls. The shape of each side wall will be a triangle with equal area.  

In the above pyramid, the base is an equilateral triangle with side length "a". 

And each wall is a triangle with base "a" and height "h"

Let us find the area of each face separately. 

Area of the base  =  (√3/4)a²

Area of each side wall  =  (1/2)ah 

Area of all 3 side walls  =  3 x (1/2)ah  =  (3/2)ah 

Surface area of the above pyramid = (√3/4)a² + (3/2)ah 

This is the formula to find surface area of a pyramid with equilateral triangle base. 

Note : If the base is not equilateral triangle and it is either scalene triangle or isosceles triangle, then the area of side walls will not be equal. We have to find area of each side wall separately.  

To have better understanding on "Surface area of 3d shapes", let us look at some practice problems

Surface area of 3d shapes - Practice problems

Problem 1 : 

Find the surface area of the cuboid given below.

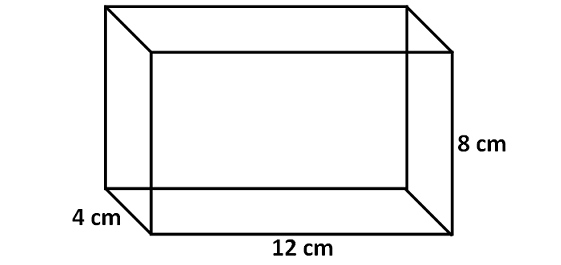
Solution : 

Surface area of cuboid   =  Sum of areas of all six faces

In cuboid, each face is a rectangle. So we can use area of rectangle formula to get area of each face. 

Area of the front face  =  8 x 12  =  96 sq. cm   

Area of the back face  =  8 x 12  =  96 sq.cm

Area of the left side face  =  4 x 8  =  32 sq.cm 

Area of the right side face  =  4 x 8  =  32 sq.cm

Area of the top portion  =  4 x 12  =  48 sq.cm

Area of the base  =  4 x 12  =  48 sq. cm

Surface area of cuboid   =  Sum of areas of all six faces

Surface area of cuboid   =  96 + 96 + 32 + 32 + 48 + 48

Surface area of cuboid   =  96 + 96 + 32 + 32 + 48 + 48

Surface area of cuboid   =  352 sq. cm

Alternative method : 

We can use the formula given below to find surface area of cuboid.

Surface area of cuboid  =  2(lh + wh + lw) 

Here, l  =  12 cm, w  =  4 cm and h  =  8 cm.

Surface area of cuboid  =  2(12x8 + 4x8 + 12x4) 

Surface area of cuboid  =  2(96 + 32 + 48)

Surface area of cuboid  =  2(176)

Surface area of cuboid  =  352 sq.cm

Let us look at the next problem on "Surface area of 3d shapes"

Problem 2 : 

Find the surface area of the cube given below.

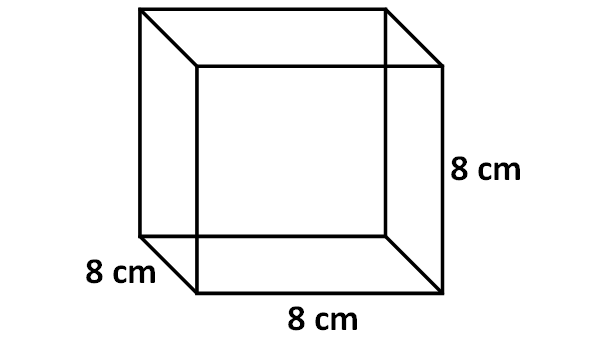
Solution :

We know that the shape of each face of a cube is a square.

In the above cube, the side length of each face is "8". 

So, area of each face (square)  =  8 x 8  =  64 sq.cm

Therefore,

surface area of the cube  =  6 x area of each face 

surface area of the cube  =  6 x 64 

Surface area of the cube  =  384  sq.cm

Let us look at the next problem on "Surface area of 3d shapes"

Problem 3 : 

Find the surface area of the triangular prism given below.

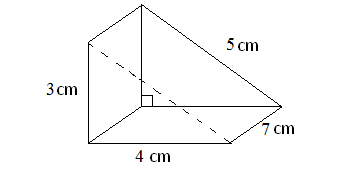
Solution :

In the above triangular prism, there are five faces. The shape of the base, vertical face and slanting face is rectangle. The shape of two faces on the left side and right side is triangle.

For the given triangular prism, 

Area of the base  =  7 x 4  =  28 sq.cm 

Area of the vertical face  =  3 x 7  = 21 sq.cm

Area of the slanting face  =  5 x 7  =  35 sq. cm

Area of the front face  =  (1/2) x 4 x 3  =  6 sq.cm

Area of the back face  =  (1/2) x 4 x 3  =  6 sq.cm

So,

surface area  =  sum of the area of 5 faces

surface area  =  28 + 21 + 35 + 6 + 6

Surface area of the triangular prism  =  96 sq.cm

Let us look at the next problem on "Surface area of 3d shapes"

Problem 4 : 

Find the surface area of the triangular prism given below.

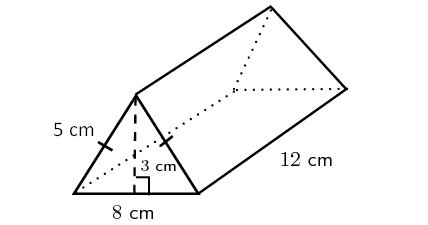
In the above triangular prism, there are five faces. The shape of the base and the two slanting faces is rectangle. The shape of two faces on the left side and right side  is triangle. 

For the given triangular prism, 

Area of the base  =  8 x 12  =  96 sq.cm 

Area of the first slanting face  =  12 x 5  = 60 sq.cm

Area of the other slanting face  =  12 x 5  =  60 sq. cm

Area of the front face  =  (1/2) x 8 x 3  =  12 sq.cm

Area of the back face  =  (1/2) x 8 x 3  =  12 sq.cm

So,

surface area  =  sum of the area of 5 faces

surface area  =  96 + 60 + 60 + 12 + 12

Surface area of the triangular prism  =  240 sq.cm

Problem 5 : 

Find the surface area of the triangular prism given below.

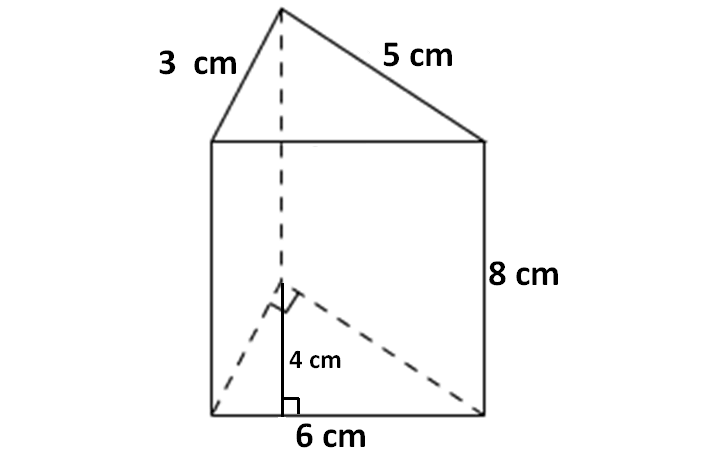
In the above triangular prism, there are five faces. The shape of the base and top portion is triangle. The shape of the faces being as side walls of the prism is rectangle. 

For the given triangular prism, 

Area of the base  =  (1/2) x 6 x 4  =  12 sq.cm 

Area of the top portion  =  (1/2) x 6 x 4  =  12 sq.cm

Area of the front face (rectangle)  =  6 x 8  =  48 sq.cm

Area of the first back face (rectangle)  =  8 x 5  =  40 sq.cm

Area of the other back face (rectangle)  =  8 x 3  =  24 sq.cm

So,

surface area  =  sum of the area of 5 faces

surface area  =  12 + 12 + 48 + 40 + 24

Surface area of the triangular prism  =  136 sq.cm

Problem 6 : 

Find the surface area of the pyramid given below.

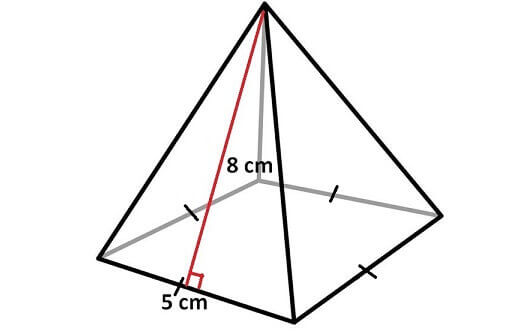
Solution : 

Surface area of the pyramid   =  Sum of areas of all 5 faces

In the above pyramid, the base is a square with side length 5 cm and each wall is a triangle with base 5 cm and height 8 cm.

Let us find the area of each face separately. 

Area of the base  =  5 x 5  =  25 sq.cm

Area of each side wall  =  (1/2) x 5 x 8  =  20 sq.cm 

Area of all 4 side walls  =  4 x 20  =  80 sq.cm 

Surface area of the above pyramid  =  25 + 80

Surface area of the above pyramid  =  105 sq.cm

Problem 7 : 

Find the surface area of the pyramid given below.

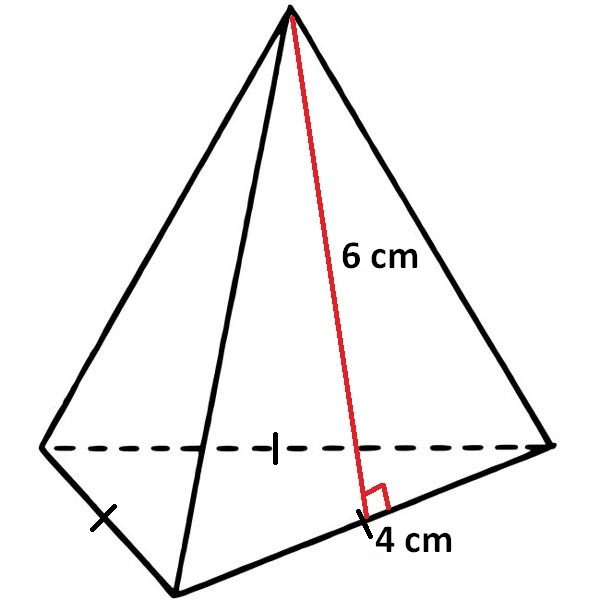
Solution : 

Surface area of the pyramid   =  Sum of areas of all 4 faces

In the above pyramid, the base is an equilateral triangle with side length 4 cm and each wall is a triangle with base 4 cm and height 6 cm.

Let us find the area of each face separately. 

Area of the base  =  (√3/4) x 4²  =  4√3 sq.cm

Area of each side wall  =  (1/2) x 4 x 6  =  12 sq.cm 

Area of all 3 side walls  =  3 x 12  =  36 sq.cm 

Surface area of the above pyramid  =  (4√3 + 36)  sq.cm

Surface area of the above pyramid  =  4(√3 + 9)  sq.cm

Problem 8 : 

Find the surface area of the pyramid given below.

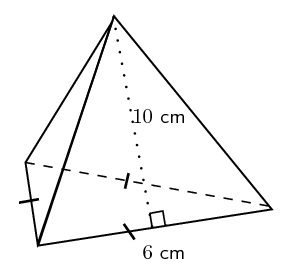
Solution : 

Surface area of the pyramid   =  Sum of areas of all 4 faces

In the above pyramid, the base is an equilateral triangle with side length 4 cm and each wall is a triangle with base 4 cm and height 6 cm.

Let us find the area of each face separately. 

Area of the base  =  (√3/4) x 6²  =  9√3 sq.cm

Area of each side wall  =  (1/2) x 6 x 10  =  30 sq.cm 

Area of all 3 side walls  =  3 x 30  =  90 sq.cm 

Surface area of the above pyramid  =  (9√3 + 90)  sq.cm

Surface area of the above pyramid  =  9(√3 + 10)  sq.cm

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.