SURFACE AREA OF PRISM AND PYRAMID WORKSHEET

Problem 1 :

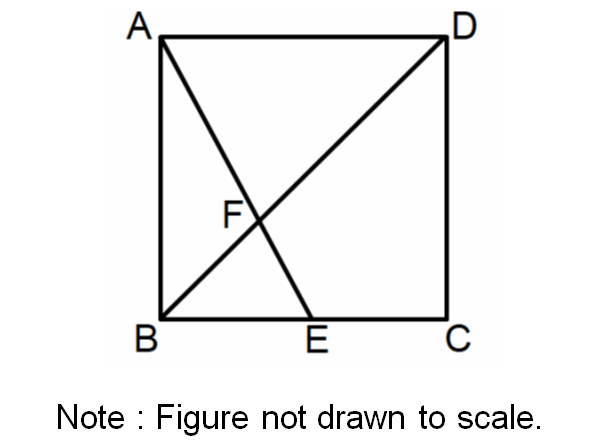
Find the surface area of the cuboid shown below.

Problem 2 :

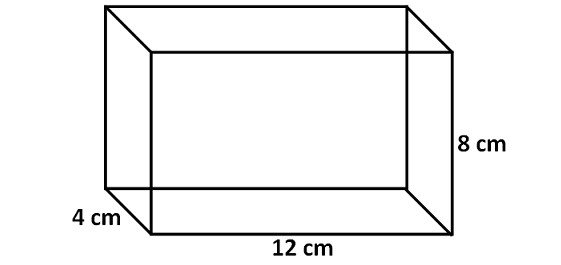
Find the surface area of the cube shown below.

Problem 3 :

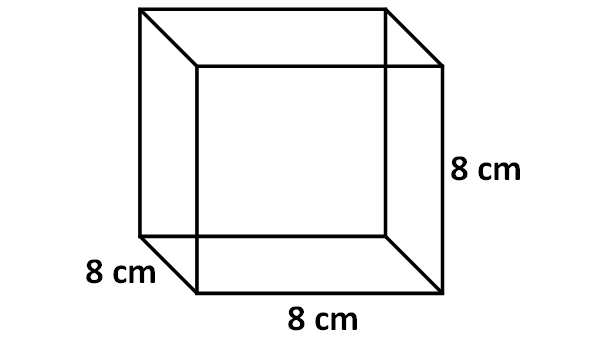
Find the surface area of the triangular prism shown below.

Problem 4 :

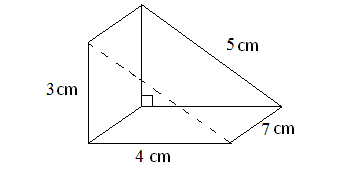
Find the surface area of the triangular prism shown below.

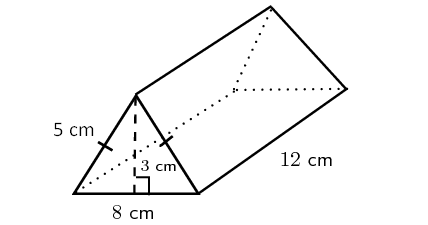
Problem 5 :

Find the surface area of the triangular prism shown below.

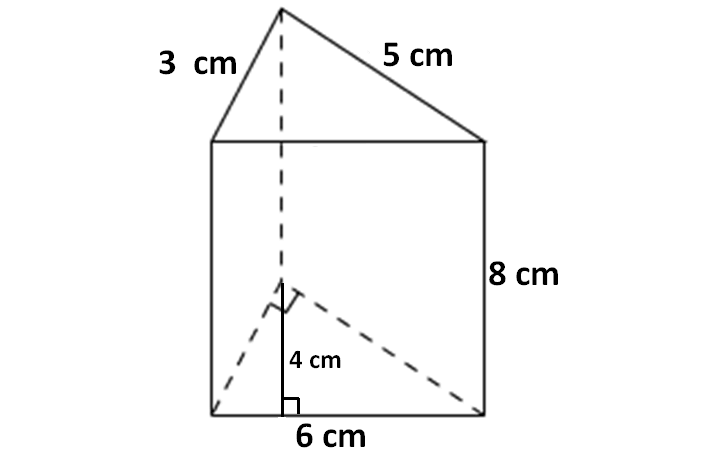
Problem 6 :

Find the surface area of the pyramid shown below.

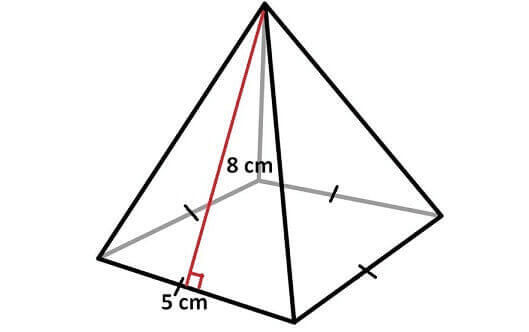
Problem 7 :

Find the surface area of the pyramid shown below.

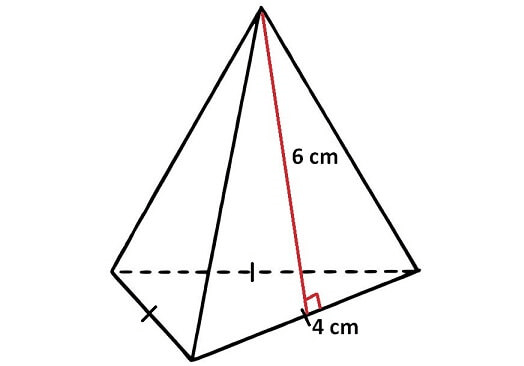
Problem 8 :

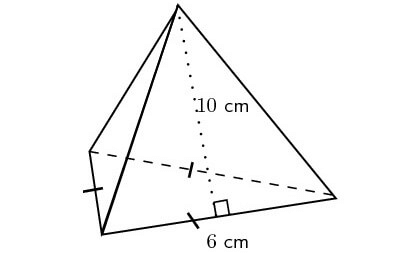
Find the surface area of the pyramid shown below.

1. Answer :

Surface area of cuboid is

=  Sum of areas of all six faces

In cuboid, each face is a rectangle. So we can use area of rectangle formula to get area of each face.

Area of the front face  =  8 x 12  =  96 cm²

Area of the back face  =  8 x 12  =  96 cm²

Area of the left side face  =  4 x 8  =  32 cm²

Area of the right side face  =  4 x 8  =  32 cm²

Area of the top portion  =  4 x 12  =  48 cm²

Area of the base  =  4 x 12  =  48 cm²

Surface area of the above cuboid is

=  Sum of areas of all six faces

=  96 + 96 + 32 + 32 + 48 + 48

=  96 + 96 + 32 + 32 + 48 + 48

=  352 cm²

Alternative Method :

We can use the formula given below to find surface area of cuboid.

Formula for surface area of cuboid is

  =  2(lh + wh + lw)

Substitute l  =  12, w  =  4 and h  =  8.

=  2(12x8 + 4x8 + 12x4)

=  2(96 + 32 + 48)

=  2(176)

=  352 cm²

2. Answer :

We know that the shape of each face of a cube is a square.

In the above cube, the side length of each face is 8.

So, area of each face (square) is

=  8 x 8

=  64 cm²

Therefore, surface area of the cube is

=  6 x area of each face

=  6 x 64

=  384  sq.cm

3. Answer :

In the above triangular prism, there are five faces. The shape of the base, vertical face and slanting face is rectangle. The shape of two faces on the left side and right side is triangle.

For the given triangular prism,

Area of the base  =  7 x 4  =  28 cm²

Area of the vertical face  =  3 x 7  =  21 cm²

Area of the slanting face  =  5 x 7  =  35 cm²

Area of the front face  =  (1/2) x 4 x 3  =  6 cm²

Area of the back face  =  (1/2) x 4 x 3  =  6 cm²

So, surface area of the above triangular prism is

=  sum of the area of 5 faces

=  28 + 21 + 35 + 6 + 6

=  96 cm²

4. Answer :

In the above triangular prism, there are five faces. The shape of the base and the two slanting faces is rectangle. The shape of two faces on the left side and right side  is triangle.

For the given triangular prism,

Area of the base  =  8 x 12  =  96 cm²

Area of the first slanting face  =  12 x 5  = 60 cm²

Area of the other slanting face  =  12 x 5  =  60 cm²

Area of the front face  =  (1/2) x 8 x 3  =  12 cm²

Area of the back face  =  (1/2) x 8 x 3  =  12 cm²

So, surface area of the above the triangular prism is

=  sum of the area of 5 faces

=  96 + 60 + 60 + 12 + 12

=  240 cm²

5. Answer :

In the above triangular prism, there are five faces. The shape of the base and top portion is triangle. The shape of the faces being as side walls of the prism is rectangle.

For the given triangular prism,

Area of the base  =  (1/2) x 6 x 4  =  12 cm²

Area of the top portion  =  (1/2) x 6 x 4  =  12 cm²

Area of the front face (rectangle)  =  6 x 8  =  48 cm²

Area of the first back face (rectangle) =  8 x 5  = 40 cm²

Area of the other back face (rectangle) = 8 x 3  =  24 cm²

So, surface area of the above the triangular prism is

=  sum of the area of 5 faces

=  12 + 12 + 48 + 40 + 24

=  136 cm²

6. Answer :

Surface area of the pyramid is

=  Sum of areas of all 5 faces

In the above pyramid, the base is a square with side length 5 cm and each wall is a triangle with base 5 cm and height 8 cm.

Let us find the area of each face separately.

Area of the base  =  5 x 5  =  25 sq.cm

Area of each side wall  =  (1/2) x 5 x 8  =  20 sq.cm 

Area of all 4 side walls  =  4 x 20  =  80 sq.cm

Surface area of the above pyramid is

=  25 + 80

=  105 sq.cm

7. Answer :

Surface area of the pyramid is

=  Sum of areas of all 4 faces

In the above pyramid, the base is an equilateral triangle with side length 4 cm and each wall is a triangle with base 4 cm and height 6 cm.

Let us find the area of each face separately.

Area of the base  =  (√3/4) x 4²  =  4√3 sq.cm

Area of each side wall  =  (1/2) x 4 x 6  =  12 sq.cm

Area of all 3 side walls  =  3 x 12  =  36 sq.cm

Surface area of the above pyramid is

=  4√3 + 36

=  4(√3 + 9)  sq. cm

8. Answer :

Surface area of the pyramid is

=  Sum of areas of all 4 faces

In the above pyramid, the base is an equilateral triangle with side length 6 cm and each wall is a triangle with base 6 cm and height 10 cm.

Let us find the area of each face separately.

Area of the base  =  (√3/4) x 6²  =  9√3 sq.cm

Area of each side wall  =  (1/2) x 6 x 10  =  30 sq.cm

Area of all 3 side walls  =  3 x 30  =  90 sq.cm

Surface area of the above pyramid is

=  (9√3 + 90)

=  9(√3 + 10)  sq.cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.