SURJECTIVE FUNCTION

Let f : A ----> B be a function.

The function f is called an onto function, if every element in B has a pre-image in A.

That is, in B all the elements will be involved in mapping. 

An onto function is also called a surjective function.

The figure given below represents a onto function.

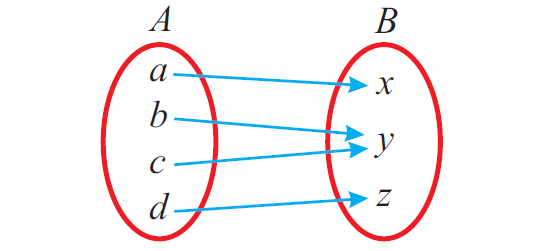
Solved Problems

Problem 1 : 

Let f : X ----> Y. X, Y and f are defined as 

X  =  {a, b, c, d}

Y  =  {d, e, f}

f  =  {(a, e), (b, f), (c, e), (d, d)}

Verify whether f is a function. if so, what type of function is f ?

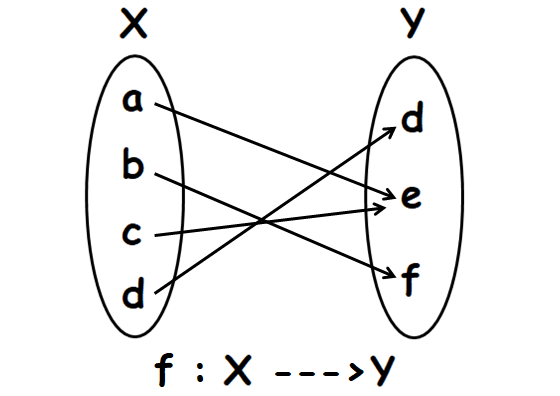
In the above arrow diagram, all the elements of X have images in Y and every element of X has a unique image.

That is, no element of X has more than one image.

So, f is a function. 

Every element of Y has a pre-image in X. 

Therefore, f is onto or surjective function. 

Problem 2 : 

Let f : A ----> B. A, B and f are defined as 

A  =  {1, 2, 3}

B  =  {5, 6, 7, 8}

f  =  {(1, 5), (2, 8), (3, 6)}

Is f surjective ? Explain. 

Solution :

Write the elements of f (ordered pairs) using arrow diagram as shown below

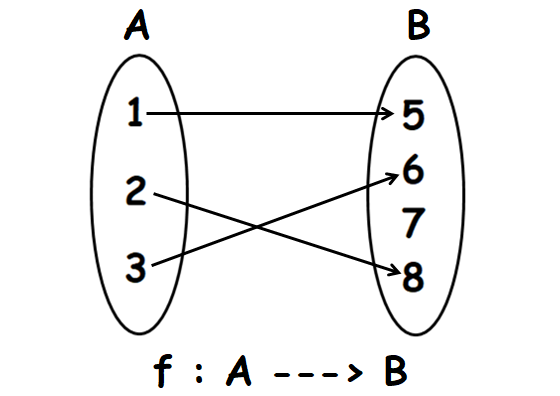
In the above arrow diagram, all the elements of A have images in B and every element of A has a unique image.

That is, no element of A has more than one image.

So, f is a function. 

The element "7" in B has no pre-image in A. 

Because the element "7" has no pre-image, f is not onto or surjective function. 

Problem 3 : 

Let f : A ----> B. A, B and f are defined as 

A  =  {1, 2, 3, 4}

B  =  {5, 6, 7, 8}

f  =  {(1, 8), (2, 6), (3, 5), (4, 7)}

Is f surjective ? Explain. 

Solution :

Write the elements of f (ordered pairs) using arrow diagram as shown below. 

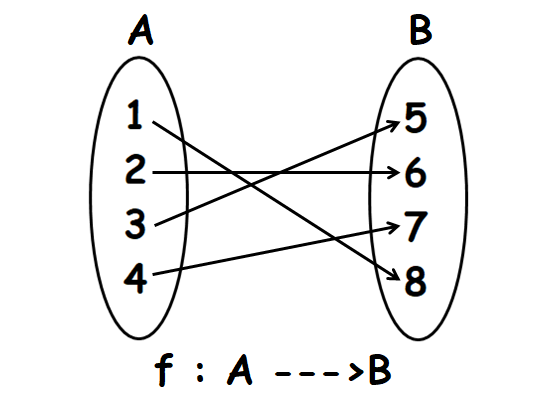
In the above arrow diagram, all the elements of A have images in B and every element of A has a unique image.

That is, no element of A has more than one image.

So, f is a function. 

Every element of B has a pre- image in A.

Therefore, f is onto or surjective function.

Related Topics

One to one or Injective function

One to one and Onto or Bijective function

Into function

Constant Function

Identity function

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.