TANGENT LINES TO CIRCLES

A tangent line intersects a circle at exactly one point, called the point of tangency. 

A line is tangent to a circle if and only if it is perpendicular to a radius drawn to the point of tangency. 

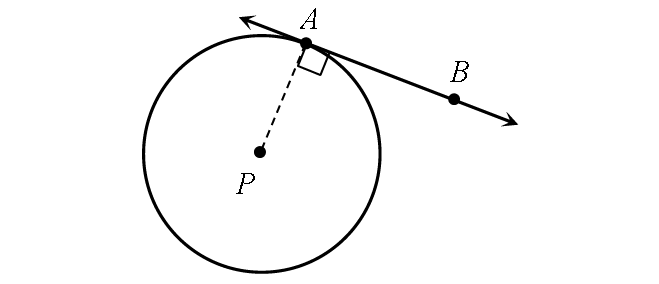
Solved Examples

Example 1 : 

Determine if the line segment AB is tangent to circle P.  

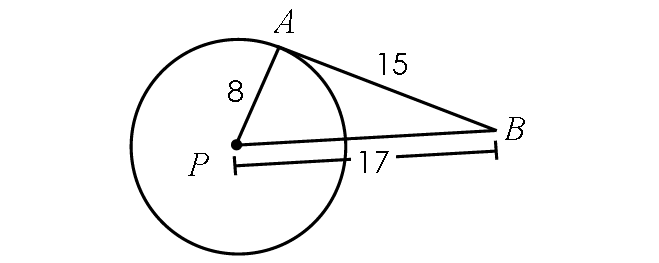
Solution : 

If the line segment AB is tangent to circle P, it is perpendicular to the radius PA.

Then, m∠PAB = 90° and triangle PAB has to be a right triangle. 

Using Pythagorean Theorem, verify whether triangle PAB is a right triangle.  

PA² + PB²  =  PB²

8² + 15²  =  17²  ?

64 + 225  =  289  ?

289  =  289  ?

The above result is true.

So, triangle PAB is a right triangle and m∠PAB = 90°.

Hence, the line segment AB is tangent to circle P.  

Example 2 : 

Determine if the line segment YX is tangent to circle Z.  

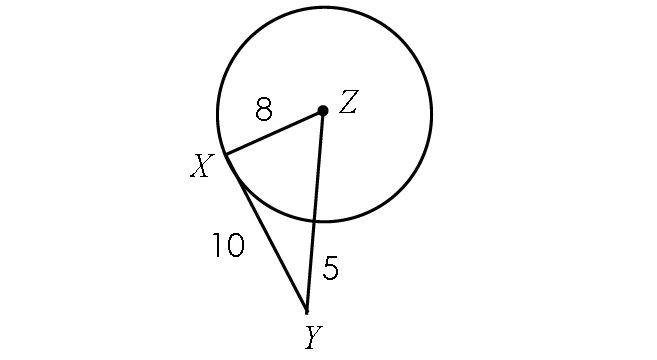
Solution : 

Find the length of ZY : 

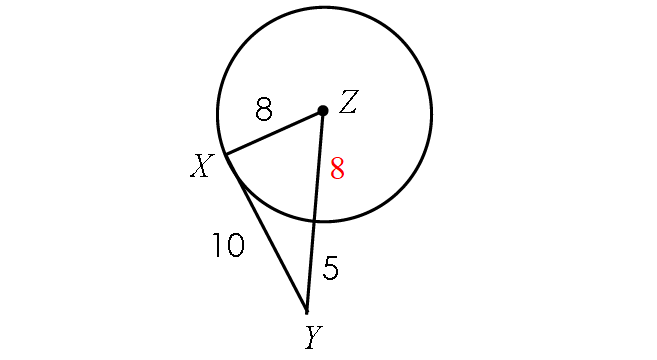
ZY  =  Radius + 5

ZY  =  8 + 5

ZY  =  13

Because the line segment YX is tangent to circle Z, it is perpendicular to the radius ZX.

Then, m∠ZXY = 90° and triangle ZXY has to be a right triangle. 

Using Pythagorean Theorem, verify whether triangle ZXY is a right triangle.  

ZX² + XY²  =  ZY²

8² + 10²  =  13²  ?

64 + 100  =  169  ?

164  =  169  ?

The above result is false.

So, triangle ZXY is not a right triangle and m∠ZXY ≠ 90°.

Hence, the line segment YX is not tangent to circle Z.  

Example 3 : 

If the line segment JK is tangent to circle L, find x.   

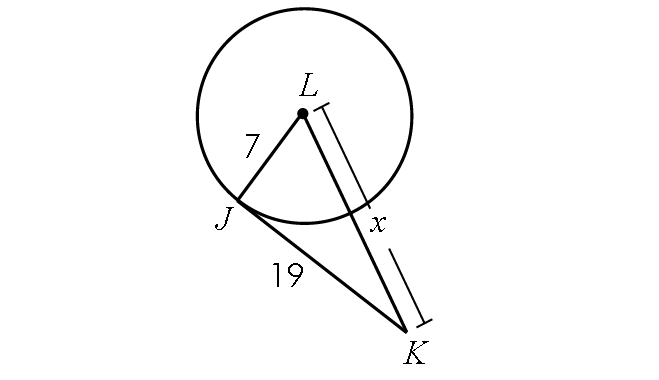
Solution : 

Because JK is tangent to circle L, m∠LJK = 90° and triangle LJK is a right triangle. 

BY Pythagorean Theorem, 

LJ² + JK²  =  LK²

7² + 19²  =  x²

49 + 361  =  x²

49 + 361  =  x²

400  =  x²

Take square root on both sides. 

20  =  x

Example 4 : 

If the line segment JK is tangent to circle L, find x.   

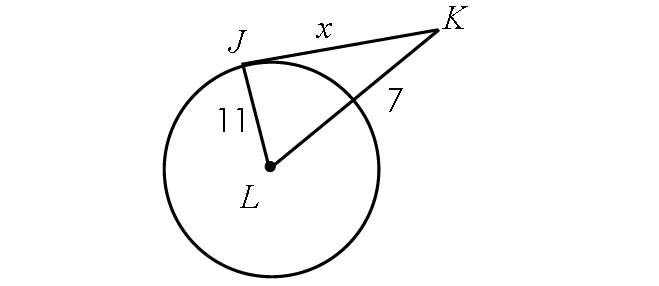
Solution : 

Find the length of LK : 

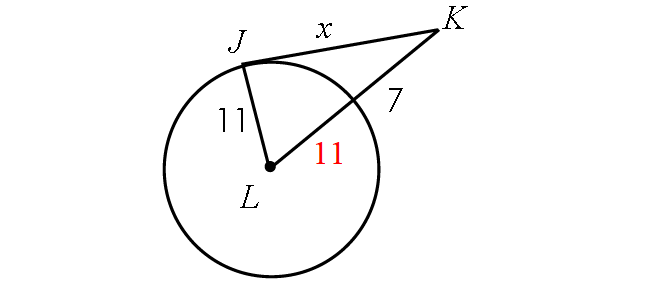
LK  =  Radius + 7

LK  =  11 + 7

LK  =  18

Because JK is tangent to circle L, m∠LJK = 90° and triangle LJK is a right triangle. 

BY Pythagorean Theorem,

LJ² + JK²  =  LK²

11² + x²  =  18²

121 + x²  =  324

Subtract 121 from each side.

x²  =  203

Take square root on both sides. 

x  ≈  14.2

Example 5 : 

If the line segment JK is tangent to circle L, find x.   

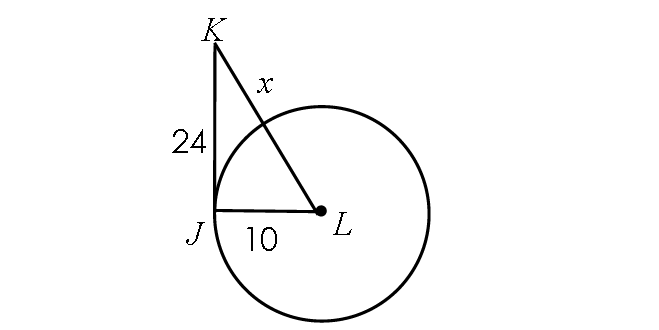
Solution : 

Find the length of LK : 

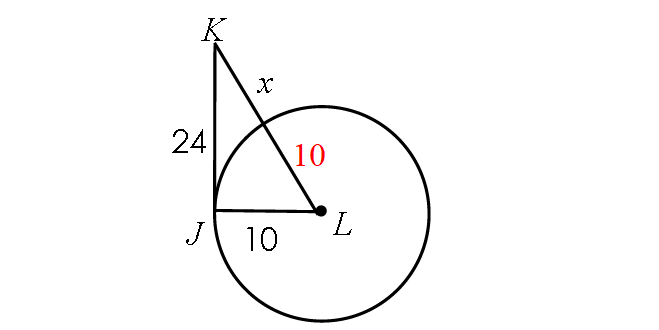
LK  =  Radius + x

LK  =  10 + x

Because JK is tangent to circle L, m∠LJK = 90° and triangle LJK is a right triangle. 

BY Pythagorean Theorem,

LJ² + JK²  =  LK²

10² + 24²  =  (10 + x)²

676  =  (10 + x)²

Take square root on both sides. 

26  =  10 + x

Subtract 10 from each side.

16  =  x

Example 6 : 

If the line segment JK is tangent to circle L, find x.   

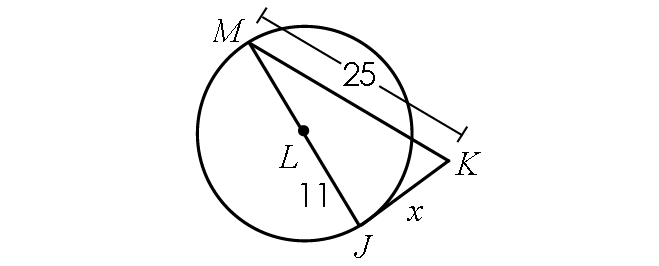
Solution : 

Find the length of JM : 

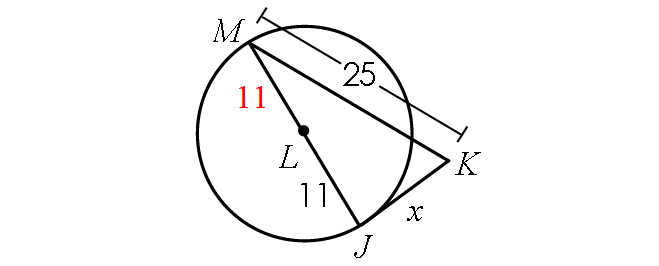
JM  =  JL + LM

JM  =  11 + 11

JM  =  22

Because JK is tangent to circle L, m∠MJK = 90° and triangle MJK is a right triangle. 

BY Pythagorean Theorem,

JM² + JK²  =  MK²

22² + x²  =  25²

484 + x²  =  625

Subtract 484 from each side.

x²  =  141

Take square root on both sides. 

x  ≈  11.9

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.