TESTS FOR SYMMETRY
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Graphs of equations can have symmetry with respect to one of the coordinate axes or with respect to the origin.
Symmetry with respect to the -axis means that if the Cartesian plane were folded along the -axis, the portion of the graph above the x-axis would coincide with the portion below the x-axis.
Symmetry with respect to the y-axis or the origin can be described in a similar manner.
X-Axis Symmetry
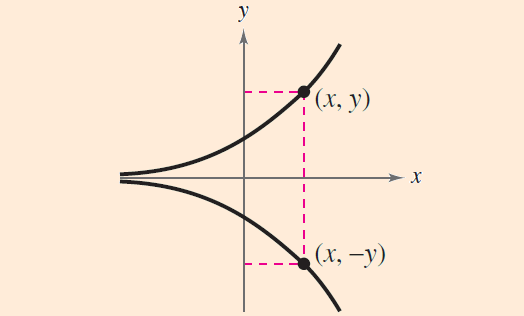
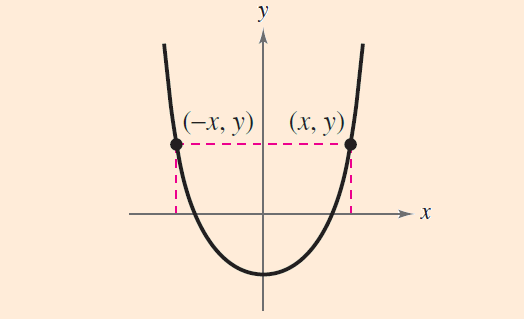
Y-Axis Symmetry
Origin Symmetry
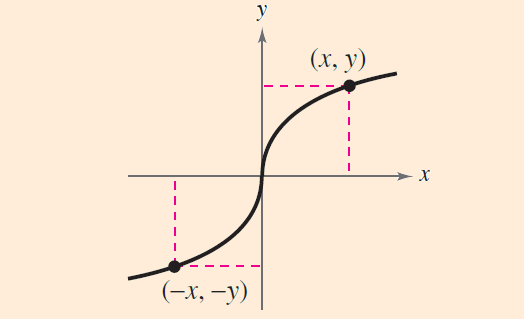
Knowing the symmetry of a graph before attempting to sketch it is helpful, because then you need only half as many solution points to sketch the graph. There are three basic types of symmetry, described as follows.
Graphical Tests for Symmetry
1. A graph is symmetric with respect to the x-axis, when the point (x, y) is on the graph, the point (x, -y) is also on the graph.
2. A graph is symmetric with respect to the y-axis, when the point (x, y) is on the graph, the point (-x, y) is also on the graph.
3. A graph is symmetric with respect to the origin, when the point (x, y) is on the graph, the point (-x, -y) is also on the graph.
Example 1 :
Prove that the graph of y = x2 - 2 is symmetric with respect to the y-axis.
Solution :
The graph of y = x2 - 2 is symmetric with respect to the y-axis.
Because, when a point (x, y) is on the graph of y = x2 - 2, the point (x , -y) is also on the graph.
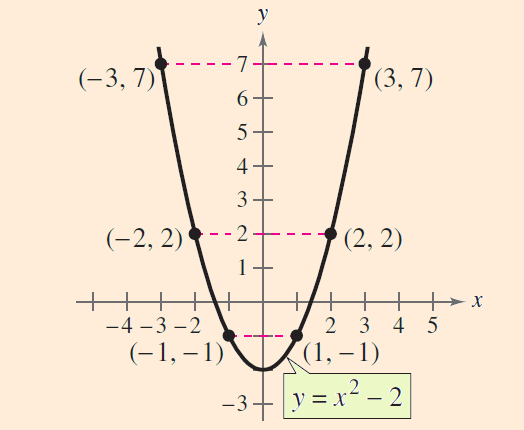
The table below confirms that the graph is symmetric with respect to the -axis
x
-3
-2
-1
1
2
3
y
7
2
-1
-1
2
7
(x, y)
(-3, 7)
(-2, 2)
(-1, -1)
(1, -1)
(2, 2)
(3, 7)
Algebraic Tests for Symmetry
1. The graph of an equation is symmetric with respect to the x-axis, if the equation is unaltered, when y is replaced -y.
2. The graph of an equation is symmetric with respect to the y-axis, if the equation is unaltered, when x is replaced -x.
3. The graph of an equation is symmetric with respect to the origin, if the equation is unaltered, when x is replaced -x and y is replaced by -y.
Example 2 :
Use symmetry to sketch the graph of
x - y2 = 1
Solution :
Of the three tests for symmetry, the only one that is satisfied is the test for x-axis symmetry.
x - y2 = 1
Replace y by -y.
x - (-y)2 = 1
x - y2 = 1
In the given equation x - y2 = 1, when y is replaced by -y, the equation is unaltered.
That is, if (x, y) is on the graph, (x, -y) also must be on the graph.
So, the graph is symmetric with respect to x-axis. Using symmetry, you only need to find the solution points above the x-axis and then reflect them to obtain the graph.
y
x = y2 + 1
(x, y)
0
1
2
1
2
5
(1, 0)
(2, 1)
(5, 2)
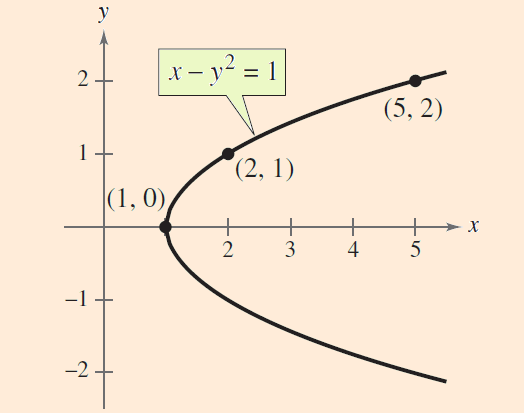
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Quantitative Reasoning Questions and Answers
Dec 13, 25 12:45 PM
Quantitative Reasoning Questions and Answers -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems -
10 Hard SAT Math Questions (Part - 39)
Dec 11, 25 05:59 PM
10 Hard SAT Math Questions (Part - 39)