THE INVERSE FUNCTION AND ITS PROPERTIES

Key Ideas : 

• The inverse of a linear function is the reverse of the original function. It undoes what the original has done and can be found using the inverse operations of the original function in reverse order.

For example, to apply the function defined by

f(x) = 3x + 4,

multiply x by 3 and then add 4. To reverse this function, subtract 4 from x and then divide the result by 3 :

f^-1(x) = (x - 8)/5

• The inverse of a function is not necessarily a function itself.

Need to Know : 

• A way to determine the inverse function is to switch the two variables and solve for the previously independent variable. For example, if y = 3x + 4, rewrite this equation as x = 3y + 4 and solve for y. 

y = (x - 4)/3

• If the original function is linear (with the exception of a horizontal line), the inverse is also a linear function.

• f^-1 is the notation for the inverse function of f.

• If (a, b) is a point on the graph of y = f(x), then (b, a) is a point on the graph of y = f^-1(x). This implies that the domain of f is the range of f^-1 and the range of f is the domain of f^-1.

• The graph of the inverse is the reflection of the graph of y = f(x) in the line y = x.

Representing the Equation of the Inverse of a Linear Function

Example 1 :

Find the inverse of the function defined by f(x) = 2 - 5x. Is the inverse a function? Explain.

Solution : (Reversing the Operations) 

In the function f(x) = 2 - 5x, the operation on x are as follows. Multiply by -5 and then add 2. 

To reverse these operations, subtract 2 and then divide the result by 25.

f^-1(x) = (x - 2)/(-5)

= - (x - 2)/5

= (-x + 2)/5

= -x/5 + 2/5

The inverse is linear, so it must be a function, since all linear relations except vertical lines are functions.

Solution : (Interchanging the Variables) 

f(x) = 2 - 5x

y = 2 - 5x

x = 2 - 5y

Solve for y. 

x - 2 = -5y

(x - 2)/(-5) = y

(x - 2)/(-5) = y

-(x - 2)/5 = y

(-x + 2)/5 = y

(2 - x)/5 = y

f^-1(x) = (2 - x)/5

The inverse is a function.

Relating the Graphs of Functions and their Inverses

Use the graph of each function to obtain the graph of the inverse. Is the inverse a function? Explain.

Example 2 : 

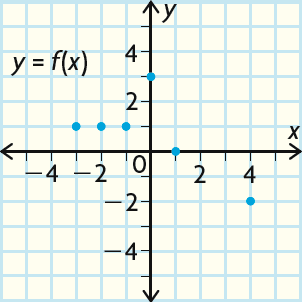
Solution : 

f(x) is a function represented by the set of points

{(-3, 1), (-2, 1), (-1, 1), (0, 3), (1, 0), (4, -2)}

So, f^-1(x) is 

{(1, -3), (1, -2), (1, -1), (3, 0), (0, 1), (-2, 4)}

Plot the points for the inverse and draw the line to check for symmetry.

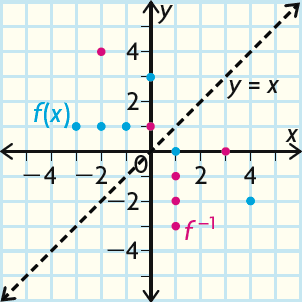
The inverse is not a function : There are three red points for x = 1, so a vertical line drawn here would go through three points. The graph fails the vertical-line test at x = 1.

Example 3 : 

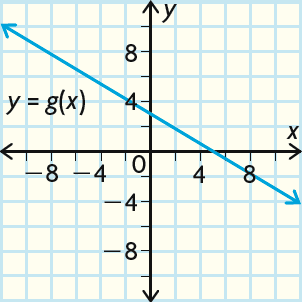
Solution : 

Write the coordinates of the x- and y-intercepts of (5, 0) and (0, 3).

Switch the coordinates to find the two points (0, 5) and (3, 0) of g^-1(x).  Notice that they were the intercepts.

Plot the two points (0, 5) and (3, 0) of g^-1(x) and join them with a straight line.

Draw the line y = x and check that the graphs of g(x) and g^-1(x) crossed on that line.

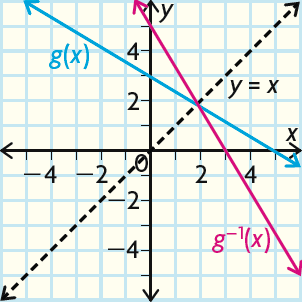
The inverse is a function because it passes the vertical-line test.

Using the Inverse of a Linear Function to Solve a Problem

Example 4 :

Earth’s surface is a function of depth and can be defined by T(d) = 11 + 0.015d.

a) State the domain and range of T(d).

b) Determine the inverse of this function.

c) State the domain and range of T^-1(d).

d) Explain what the inverse represents.

Solution : 

(a) :

d is 0 m on the surface. This is the beginning of the domain. The deeper mine has a depth of 4100 m, the domain ends at 5000.

Domain = {d ∊ R | 0 ≤ d ≤ 5000}

To calculate the beginning and end of the range substitute d = 0 and d = 5000 into the equation for T(d). 

T(0) = 11 + 0.015(0) = 11 + 0 = 11

T(5000) = 11 + 0.015(5000) = 11 + 75 = 86

Range = {T(d) ∊ R | 0 ≤ T(d) ≤ 86}

(b) : 

T(d) = 11 + 0.015d

Replace T(d) by y and d by x. 

y = 11 + 0.015x

Interchange the variables. 

x = 11 + 0.015y

Solve for y. 

x - 11 = 0.015y

(x - 1)/0.015 = y

d(T) = (T - 11)/0.015 is the inverse function. 

(c) :

The domain of the inverse is the same as the range of the original function, and the range of the inverse is the same as the domain of the original function.

Domain = {T ∊ R | 11 ≤ T ≤ 86}

Range = {d(T) ∊ R | 0 ≤ d(T) ≤ 5000}

(d) :

The inverse shows the depth as a function of the temperature.

d(20) = (20 - 11)/0.015

= 9/0.015

= 600

When the temperature is the depth is about 733 m. 

Properties of Inverse Function

1.  A function, say f is invertible if and only if f is one to one onto.

For example, if f and g are two functions inverse to each other, then both f and g are one to one onto functions.  

2. If f(x) and g(x) are the two functions which are inverse to each other, then we have 

f^-1(x)  =  g(x) and also g^-1(x)  =  f(x)

3.  f(x) and g(x) are the two functions which are inverse to each other, if and only if  

f o g = g o f = x

4.  Let f(x) be a function such that f : A --> B and g be the inverse of f. Then we have 

g : B --> A

5.  Let f and g be the two functions which are inverse to each other. Then we have

Domain of f(x) = Range of g(x)

Range of f(x) = Domain of g(x)

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.