THE LANGUAGE AND TOOLS OF ALGEBRA

Variables and Expressions

In algebra, variables are symbols used to represent unspecified numbers or values. An algebraic expression is a collection of numbers, variables, operations, and grouping symbols.

Addition :

Subtraction :

Multiplication :

Division :

Exponents and Order of Operations

An expression like 5³ is called a power. The number 5 is the base and 3 is the exponent.

5³ = 5 ⋅ 5 ⋅ 5

In evaluating the power of 5³, we have 3 factors of 5.

To evaluate an expression involving more than one operation, we agree to perform operations in the following order .

Order of Operations :

1. Simplify the expressions inside grouping symbols, such as parentheses, brackets, and fraction bars.

2. Evaluate all powers.

3. Do all multiplications and divisions in order from left to right.

4. Do all additions and subtractions in order from left to right.

Example 1 :

Evaluate :

[(7² - 9) ÷ 8]2

Solution :

= [(7² - 9) ÷ 8]2

Evaluate power inside grouping symbols.

= [(49 - 9) ÷ 8]2

Evaluate expression inside grouping symbols.

= [40 ÷ 8]2

Divide 40 by 8.

= [5]2

Multiply 5 and 2.

= 10

Example 2 :

Evaluate :

{11 - 20 ÷ [(5² - 13)/3] + 8} ⋅ 2

Solution :

= {11 - 20 ÷ [(5² - 13)/3] + 8} ⋅ 2

Evaluate power inside grouping symbols.

= {11 - 20 ÷ [(25 - 13)/3] + 8} ⋅ 2

Evaluate expression inside grouping symbols.

= {11 - 20 ÷ [12/3] + 8} ⋅ 2

Evaluate expression inside grouping symbols.

= {11 - 20 ÷ 4 + 8} ⋅ 2

Divide 20 by 4.

= {11 - 5 + 8} ⋅ 2

Subtract 5 from 11.

= {6 + 8} ⋅ 2

Evaluate expression inside grouping symbols.

= 14 ⋅ 2

Multiply.

= 28

Simplifying Algebraic Expressions

A term is a number, a variable, or a product or quotient of numbers and variables.

For example 7, x, 3a, b² and 2m²n are all terms.

Like terms contain identical variables.

For example, in 7x² - 4x² + 3x, the terms 7x² and -4x² are like terms, because the variable part of each term is identical.

The coefficient of a term is a number that multiplies a variable.

For example, in 9x²y, the coefficient is 9. and in 3m/5, the coefficient is 3/5.

An expression is in simplest form when it is replaced by an equivalent expression having no like terms or parentheses. Simplifying means rewriting in simpler form.

Distributive Property :

For any real numbers a, b and c,

a(b + c) = ab + ac

a(b - c) = ab - ac

Commutative Property :

For any real numbers a and b,

a + b = b + a

a ⋅ b = b ⋅ a

Associative Property :

For any real numbers a, b and c,

(a + b) + c = a + (b + c)

(a ⋅ b) ⋅ c = a ⋅ (b ⋅ c)

Example 3 :

Simplify :

m/3 - 4n + 8m/3

Solution :

= m/3 - 4n + 8m/3

Combine like terms.

= (m + 8m)/3 - 4n

Simplify.

= 9m/3 - 4n

= 3m - 4n

Example 4 :

Simplify :

4x³ - 2(x³ + 3x)

Solution :

= 4x³ - 2(x³ + 3x)

Using Distributive Property,

= 4x³ - 2(x³) - 2(3x)

= 4x³ - 2x³ - 6x

Combine like terms.

= 2x³ - 6x

Example 5 :

Simplify :

a(2 - b) - 2(a - b)

Solution :

= a(2 - b) - 2(a - b)

Using Distributive Property,

= a(2) + a(-b) - 2(a) - 2(-b)

= 2a - ab - 2a + 2b

Using Commutative property,

= 2a - 2a - ab + 2b

= -ab + 2b

Rational Irrational and Decimal

Numbers can be pictured as points on a horizontal line called a number line. The point for 0 is the origin. Points to the left of 0 represent negative numbers, and points to the right of 0 represent positive numbers. Numbers increase in value from left to right.

The point that corresponds to a number is called the graph of the number. Each number in a pair such as 3 and -3 is called the opposite of the other number. The opposite of 'a' is written '-a'.

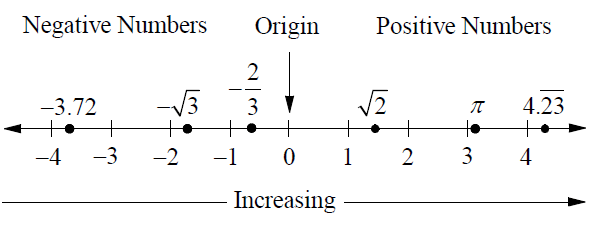
Natural Numbers :

{1, 2, 3, ...........}

Whole Numbers :

{0, 1, 2, 3, ...........}

Integers :

{........... , -3, -2, -1, 0, 1, 2, 3, ...........}

Rational Numbers : 

A rational number is the one that can be expressed as a ratio a/b, where 'a' and 'b' are integers b ≠ 0. The decimal form of a rational number is either terminating or repeating decimal, such as 

-3.72, -2/3, 0.2 and 4.2323..........

Irrational Numbers : 

Any real number that is not rational is irrational.

-√3, √2 and π are irrational

√a is considered as irrational when 'a' is not a perfect square.

If you have square root of a number, it may be rational or irrational. To determine the square root of a number is rational or irrational, check the number inside the square root is a perfect square or NOT a perfect square.

If the number inside the square root is a perfect square, then the square root of the given number is rational.

If the number inside the square root is NOT a perfect square, then the square root of the given number is irrational.

For example.

√25 is a rational, because 25 is a perfect square

√25 = 5 (rational)

√10 is an irrational, because 10 is NOT a perfect square

√10 = 3.16227........ (irrational)

3.16227........ is a non terminating and non repeating decimal. So, 3.16227........ is an irrational number.

Rounding Decimals

in the place to be rounded.

1. If the digit to the right of the underlined digit is 5 or more, increase the underlined digit by one (round up).

2. If the digit to the right of the underlined digit is less than 5, leave the underlined digit as it is (round down).

3. Drop all digits to the right of the underlined digit.

Example 6 :

Round 52.348 to the nearest

a) integer and b) hundredth.

Solution :

Part (a) :

Underline 2, the digit in the ones place. 52.348

The digit to the right of the underlined digit is less than 5, keep the underlined digit as it is.

Therefore, 52.348 rounded to the nearest integer is 52.

Part (b) :

Underline 4, the digit in the hundredths place. 52.348

The digit to the right of the underlined digit is more than 5, round up.

Therefore, 52.348 rounded to the nearest hundredths place is 52.35.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.