TRANSITIVE RELATION

Let us consider the set A as given below.

A  =  {a, b, c}

Let R be a transitive relation defined on the set A. 

Then,

R  =  { (a, b), (b, c), (a, c)}

That is,

If "a" is related to "b" and "b" is related to "c", then "a" has to be related to "c".  

In simple terms,

a R b, b R c -----> a R c

Example :

Let A  =  { 1, 2, 3 } and R be a relation defined on  set A as "is less than" and R  = {(1, 2), (2, 3), (1, 3)} Verify R is transitive. 

Solution :

From the given set A, let

a  =  1

b  =  2

c  =  3

Then, we have

(a, b)  =  (1, 2) -----> 1 is less than 2 

(b, c)  =  (2, 3) -----> 2 is less than 3 

(a, c)  =  (1, 3) -----> 1 is less than 3 

That is, if 1 is less than 2 and 2 is less than 3, then 1 is less than 3. 

More clearly, 

1R2, 2R3 -----> 1R3

Clearly, the above points prove that R is transitive. 

Important Note :

For a particular ordered pair in R, if we have (a, b) and we don't have (b, c), then we don't have to check transitive for that ordered pair. 

So, we have to check transitive, only if we find both (a, b) and (b, c) in R. 

Solved Problems

Problem 1 :

Let A  =  {1, 2, 3} and R be a relation defined on set A as

R  = {(1, 1), (2, 2), (3, 3), (1, 2)}

Verify R is transitive. 

Solution :

To verify whether R is transitive, we have to check the condition given below for each ordered pair in R.

That is, 

(a, b),  (b, c) -----> (a, c)

Let's check the above condition for each ordered pair in R. 

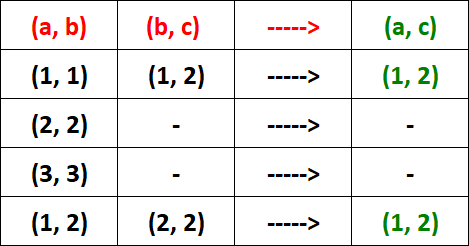
From the table above, it is clear that R is transitive. 

Note : 

For the two ordered pairs (2, 2) and (3, 3), we don't find the pair (b, c). So, we don't have to check the condition for those ordered pairs.  

Problem 2 :

Let A  =  {1, 2, 3} and R be a relation defined on set A as

R  = {(1, 1), (2, 2), (1, 2), (2, 1)}

Verify R is transitive. 

Solution :

To verify whether R is transitive, we have to check the condition given below for each ordered pair in R.

That is, 

(a, b),  (b, c) -----> (a, c)

Let's check the above condition for each ordered pair in R. 

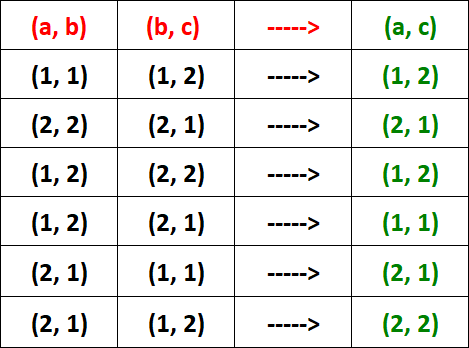
From the table above, it is clear that R is transitive. 

Problem 3 :

Let A  =  {1, 2, 3} and R be a relation defined on set A as

R  = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (2, 3), (3, 2)}

Verify R is transitive. 

Solution :

To verify whether R is transitive, we have to check the condition given below for each ordered pair in R.

That is, 

(a, b), (b, c) -----> (a, c)

Let's check the above condition for each ordered pair in R. 

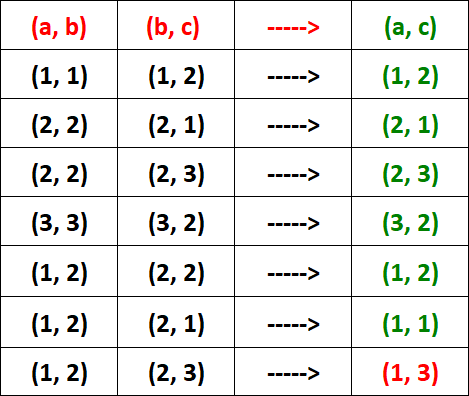
In the table above, for the ordered pair (1, 2), we have both (a, b) and (b, c). But, we don't find (a, c). 

That is, we have the ordered pairs (1, 2) and (2, 3) in R. But, we don't have the ordered pair (1, 3) in R. 

So, we stop the process and conclude that R is not transitive. 

Related Topics

Reflexive relation

Symmetric relation

Equivalence relation

Identity relation

Inverse relation

Difference between reflexive and identity relation

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.