TRANSLATIONS IN A COORDINATE PLANE

Translations in a coordinate plane can be described by the following coordinate notation :

(x, y) ----> (x + a, y + b)

where a and b are constants. Each point shifts a units horizontally and b units vertically. 

Example 1 : 

Describe the translation in the coordinate plane shown below. 

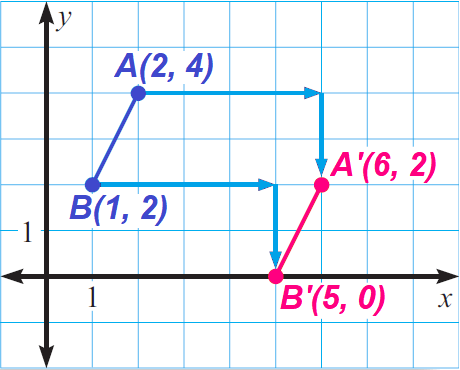
Solution :

In the coordinate plane shown above, the translation is

(x, y) ----> (x + 4, y - 2)

That is, the translation in the coordinate plane above shifts each point 4 units to the right and 2 units down. 

Example 2 :

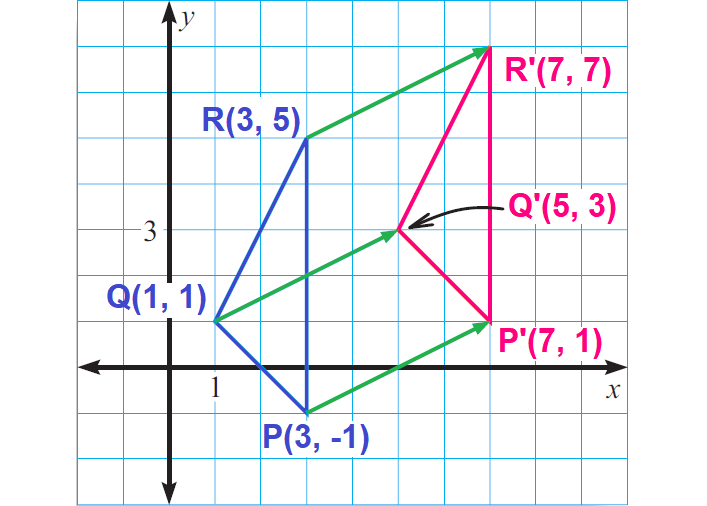
Sketch a triangle with vertices P(3, -1), Q (1, 1) and R(3, 5). Then sketch the image of the triangle after a translation to the right by 4 units and up by 2 units. 

Solution : 

First graph ΔPQR.

We have to do a translation to the right by 4 units and up by 2 units.

So the image vertices should all be 4 units to the right and 2 units up from the preimage vertices.

That is, 

P(3, 1) ----> (3 + 4, - 1 + 2) ----> P'(7, 1)

Q(1, 1) ----> (1 + 4, 1 + 2) ----> P'(5, 3)

R(3, 5) ----> (3 + 4, 5 + 2) ----> P'(7, 7)

Label the image vertices P'(7, 1), Q'(5, 3), and R'(7, 7). Then, using a straightedge, draw ΔP'Q'R'.

Example 3 : 

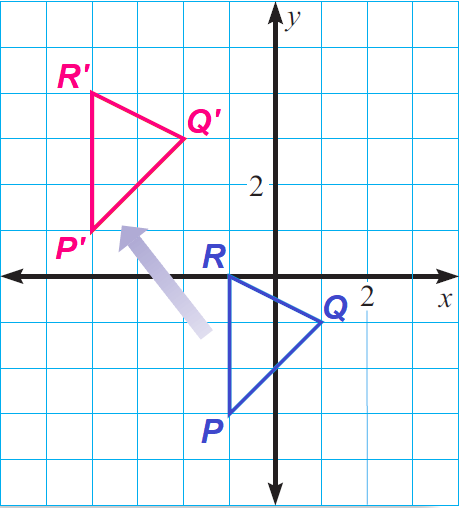
Sketch a triangle with vertices A(- 1, - 3), B(1, - 1), and C( - 1, 0). Then sketch the image of the triangle after the translation (x, y) ----> (x - 3, y + 4). 

Solution : 

First graph ΔABC.

From (x, y) ----> (x - 3, y + 4), it is clear that we have to do a translation to the left by 3 units and up by 4 units.

So the image vertices should all be 3 units to the left and 4 units up from the preimage vertices.

That is, 

P(- 1, - 3) ----> (- 1 - 3, - 3 + 4) ----> P'(- 4, 1)

Q(1, - 1) ----> (1 - 3, - 1 + 4) ----> Q'(- 2, 3)

R(- 1, 0) ----> (- 1 - 3, 0 + 4) ----> R'(- 4, 4)

Label the image vertices P'(- 4, 1), Q'(- 2, 3), and R'(- 4, 4). Then, using a straightedge, draw ΔP'Q'R'.

Example 4 :

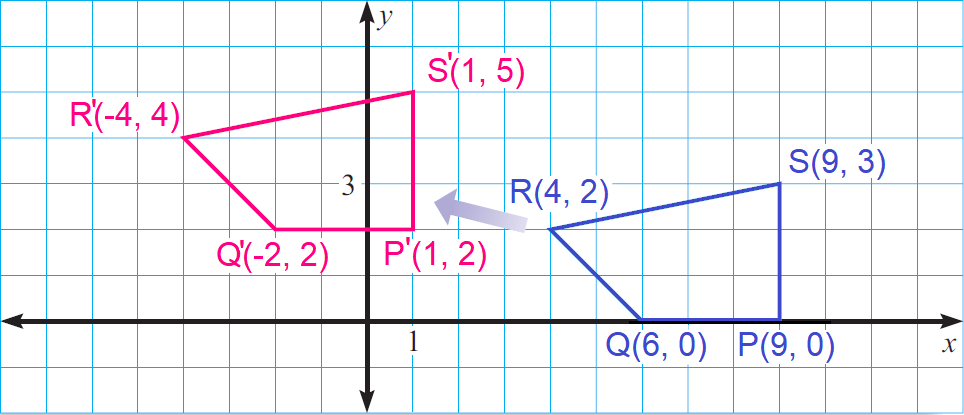
In the diagram shown below, QRST maps onto Q'R'S'T' by a translation. Write the component form of the vector that can be used to describe the translation.

Solution :

Choose any vertex and its image, say R and R'. To move from R to R', we have to move 8 units to the left and 2 units up.

So, the component form of the vector is

〈-8, 2〉

Example 5 :

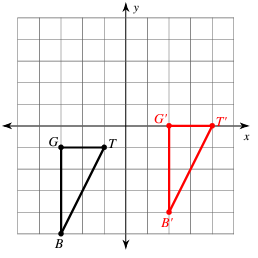
Graph the image of the figure using the transformation given.

translation: 5 units right and 1 unit up

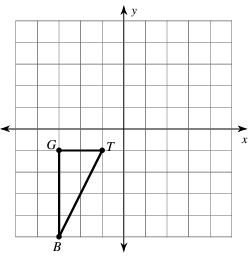
Solution :

Finding the coordinates G (-3, -1), T (-1, -1) and B (-3, -5). Original points will be in the form of (x, y). After translation point will be in the form (x + h, y + k)

Here

• h = horizontally right of 5 units, then +5
• k = vertically 1 unit up, then +1

The new point will be (x + 5, y + 1)

• G (-3, -1) ==> G'(-3 + 5, -1 + 1) ==> G'(2, 0)
• T (-1, -1) ==> T'(-1 + 5, -1 + 1) ==> T'(4, 0)
• B (-3, -5) ==> T'(-3 + 5, -5 + 1) ==> T'(2, -4)

Example 6 :

translation: 1 unit left and 2 units up

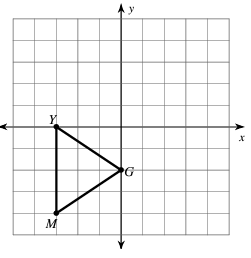
Solution :

Finding the coordinates G (-3, 0), T (0, -2) and M (-3, -4). Original points will be in the form of (x, y). After translation point will be in the form (x + h, y + k)

Here

• h = horizontally left of 1 unit, then -1
• k = vertically 2 units up, then +2

The new point will be (x - 1, y + 2)

• G (-3, 0) ==> G'(-3 - 1, 0 + 2) ==> G'(-4, 2)
• G (0, -2) ==> G'(0 - 1, -2 + 2) ==> G'(-1, 0)
• T (-3, -4) ==> T'(-3 - 1, -4 + 2) ==> T'(-4, -2)

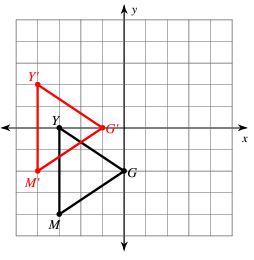
Example 7 :

Write a rule to describe each transformation.

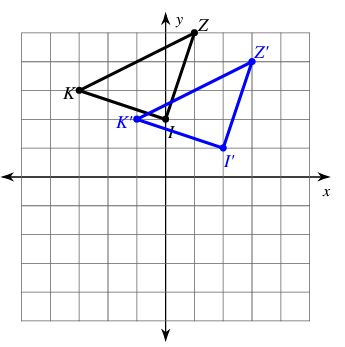
Points in the preimage are :

Z (1, 5), K (-3, 3) and I (0, 2)

Points in the image are :

Z' (3, 4), K' (-1, 2) and I' (2, 1)

Comparing the x-coordinate and y-coordinate of in Z and Z', we get

1 + 2 ==> 3

5 - 1 ==> 4

Comparing the x-coordinate and y-coordinate of in K and K', we get

-3 + 2 ==> -1

3 - 1 ==> 2

Comparing the x-coordinate and y-coordinate of in I and I', we get

0 + 2 ==> 2

2 - 1 ==> 1

Moving the graph 2 units right and 1 unit down.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.