TRANSLATIONS IN COORDINATE PLANE WORKSHEET

Problem 1 :

Describe the translation in the coordinate plane shown below. 

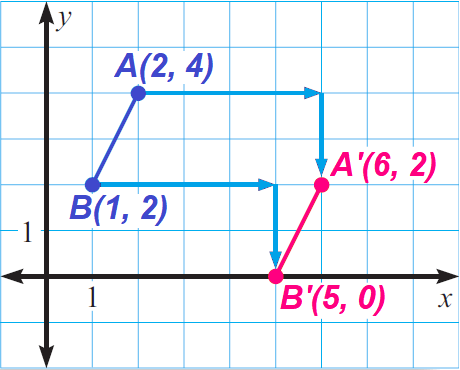
Problem 2 : 

Sketch a triangle with vertices P(3, -1), Q (1, 1) and R(3, 5). Then sketch the image of the triangle after a translation to the right by 4 units and up by 2 units.

Problem 3 :

Sketch a triangle with vertices A(- 1, - 3), B(1, - 1), and C( - 1, 0). Then sketch the image of the triangle after the translation (x, y) ----> (x - 3, y + 4). 

Problem 4 :

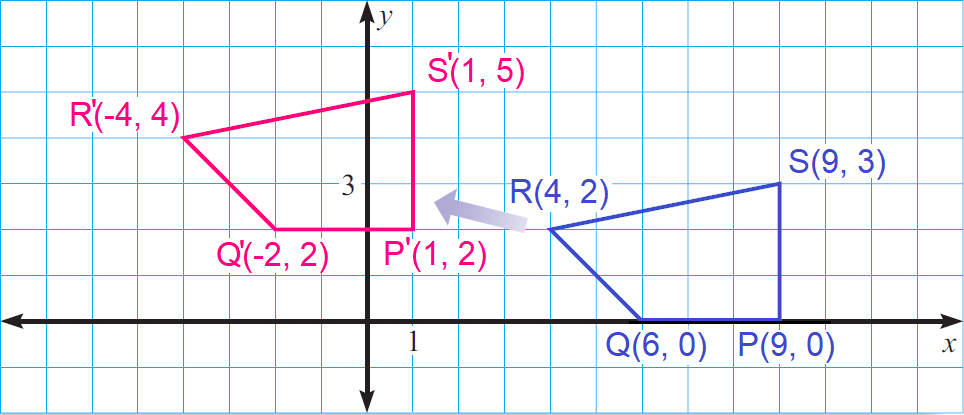
In the diagram shown below, QRST maps onto Q'R'S'T' by a translation. Write the component form of the vector that can be used to describe the translation.

Detailed Answer Key

Problem 1 :

Describe the translation in the coordinate plane shown below. 

Solution :

In the coordinate plane shown above, the translation is

(x, y) ----> (x + 4, y - 2)

That is, the translation in the coordinate plane above shifts each point 4 units to the right and 2 units down. 

Problem 2 : 

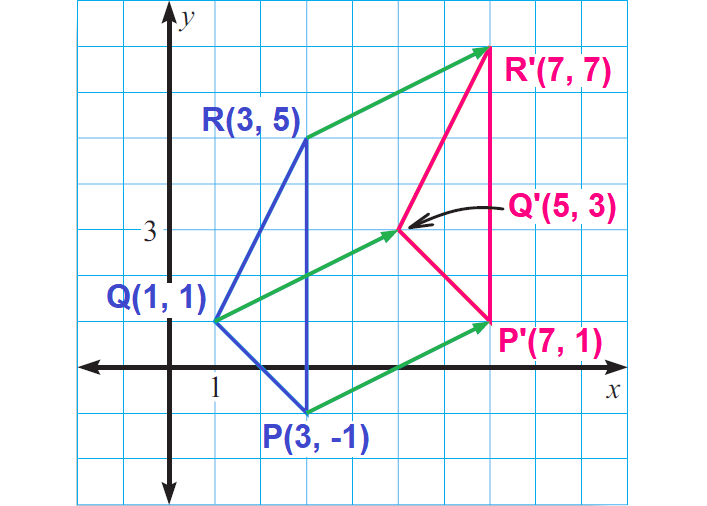
Sketch a triangle with vertices P(3, -1), Q (1, 1) and R(3, 5). Then sketch the image of the triangle after a translation to the right by 4 units and up by 2 units. 

Solution : 

First graph ΔPQR.

We have to do a translation to the right by 4 units and up by 2 units.

So the image vertices should all be 4 units to the right and 2 units up from the preimage vertices.

That is, 

P(3, 1) ----> (3 + 4, - 1 + 2) ----> P'(7, 1)

Q(1, 1) ----> (1 + 4, 1 + 2) ----> P'(5, 3)

R(3, 5) ----> (3 + 4, 5 + 2) ----> P'(7, 7)

Label the image vertices P'(7, 1), Q'(5, 3), and R'(7, 7). Then, using a straightedge, draw ΔP'Q'R'.

Problem 3 :

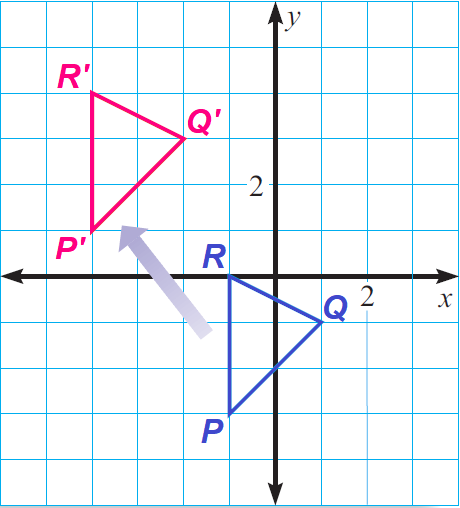
Sketch a triangle with vertices A(- 1, - 3), B(1, - 1), and C( - 1, 0). Then sketch the image of the triangle after the translation (x, y) ----> (x - 3, y + 4). 

Solution : 

First graph ΔABC.

From (x, y) ----> (x - 3, y + 4), it is clear that we have to do a translation to the left by 3 units and up by 4 units.

So the image vertices should all be 3 units to the left and 4 units up from the preimage vertices.

That is, 

P(- 1, - 3) ----> (- 1 - 3, - 3 + 4) ----> P'(- 4, 1)

Q(1, - 1) ----> (1 - 3, - 1 + 4) ----> Q'(- 2, 3)

R(- 1, 0) ----> (- 1 - 3, 0 + 4) ----> R'(- 4, 4)

Label the image vertices P'(- 4, 1), Q'(- 2, 3), and R'(- 4, 4). Then, using a straightedge, draw ΔP'Q'R'.

Problem 4 :

In the diagram shown below, QRST maps onto Q'R'S'T' by a translation. Write the component form of the vector that can be used to describe the translation.

Solution :

Choose any vertex and its image, say R and R'. To move from R to R', we have to move 8 units to the left and 2 units up.

So, the component form of the vector is

〈-8, 2〉

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.