TRIANGLE CONGRUENCE AND SIMILARITY

Congruent Triangles :

Two triangles are congruent if they have the same three sides and exactly the same three angles.

In other words, the corresponding sides of two congruent triangles are equal in length and their corresponding angles are equal. When the two congruent triangles are moved or rotated in any direction, they will have the same shape and size and will still be congruent to one another.

Congruent triangles will remain congruent even on reflecting them to get mirror their image. That is, in any case, their sides and angles will be same as their congruent triangles.

Similar Triangles :

Two triangles are said to be similar, if they have same shape, but different in sizes.

In other words, we can say that the proportions of their sides are same. Same proportion indicates that their shape must be same, but sizes can be different. If we rotate, move, reflect, or even change the scale of a shape, then it will be similar to the same shape it was before.

Rules for Two Triangles to be Congruent

Rule 1 : SSS (Side, Side, Side)

Two triangles can be congruent, if all the three sides of a triangle are equal to the corresponding sides of another.

This rule is thus known as side, side, side or in short SSS principle.

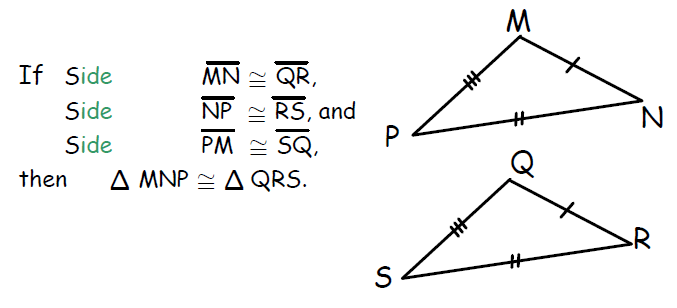
Rule 2 : SAS (Side, Angle, Side)

Two triangles are said to be congruent, if two sides of a triangle are equal to corresponding sides of another and angle between them is also of same measure. For this criterion, It is mandatory that the angle to be considered is the angle between the equal sides.

This rule is known as side, angle, side or SAS rule.

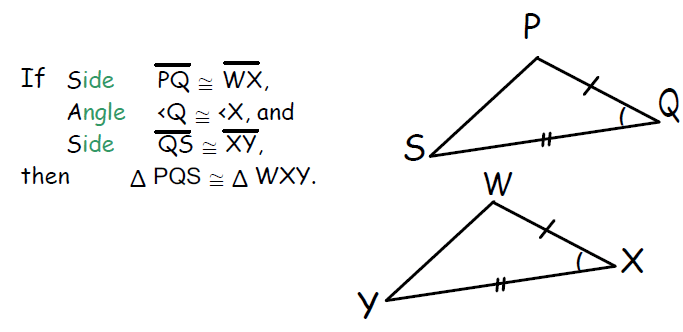
Rule 3 : AAS (Angle, Angle, Side)

If in two triangles, two corresponding angles are equal in measure and one corresponding side is equal in length, then these triangles are said to be congruent to each other.

This principle is known as angle, angle, side or AAS principle.

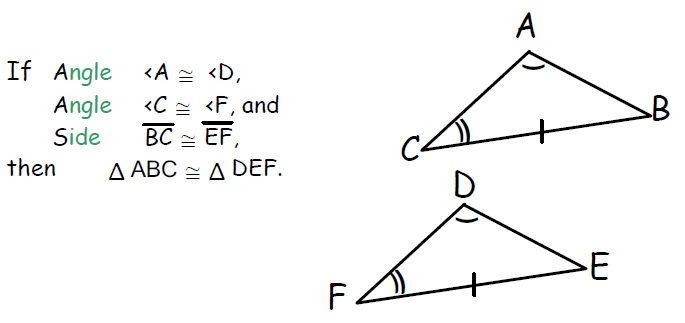
Rule 4 : ASA (Angle, Side, Angle)

If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.

This principle is known as angle, side, angle or ASA principle.

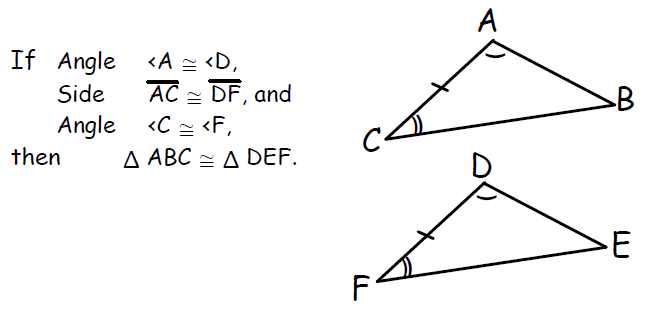
Rule 5 : Hypotenuse-Leg (HL) Theorem

If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent.

This principle is known as Hypotenuse-Leg theorem.

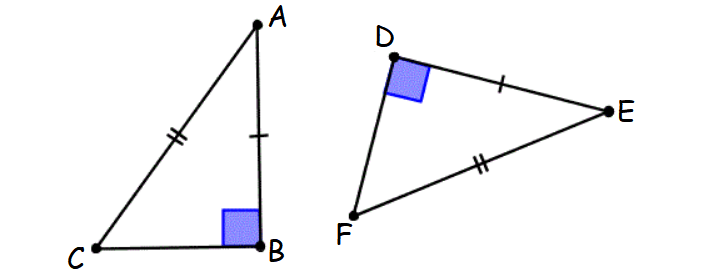
Rule 6 : Leg-Acute (LA) Angle Theorem

If a leg and an acute angle of one right triangle are congruent to the corresponding parts of another right triangle, then the two right triangles are congruent.

This principle is known as Leg-Acute Angle theorem.

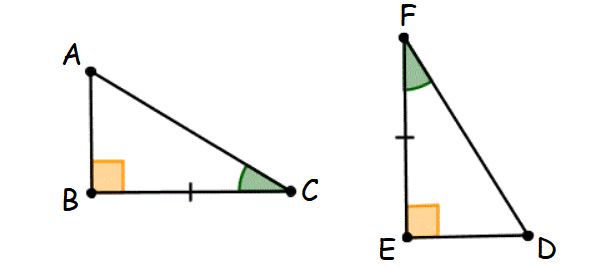
Rule 7 : Hypotenuse-Acute (HA) Angle Theorem

If the hypotenuse and an acute angle of a right triangle are congruent to the hypotenuse and an acute angle of another right triangle, then the two triangles are congruent.

This principle is known as Hypotenuse-Acute Angle theorem.

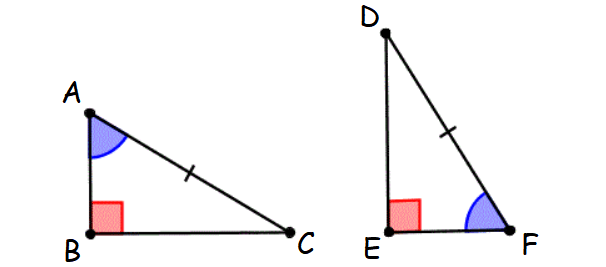
Rule 8 : Leg-Leg (LL) Theorem

If the legs of one right triangle are congruent to the legs of another right triangle, then the two right triangles are congruent.

This principle is known as Leg-Leg theorem.

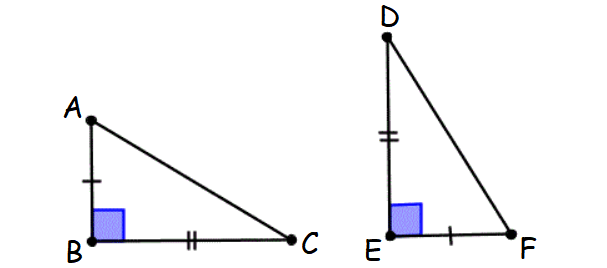
Rules for Two Triangles to be Similar

Rule 1 : AA (Angle, Angle)

If two angles in one triangle are equal to the corresponding angles in another triangle, then both triangles would be similar to each other.

This is called angle, angle or AA criterion.

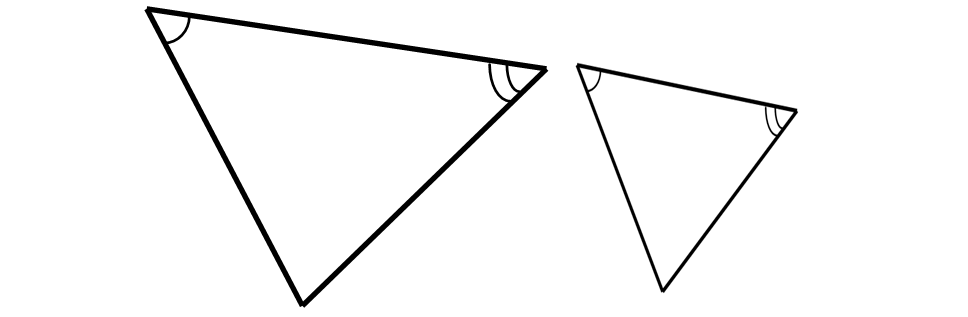
Rule 2 : SSS (Side, Side, Side)

If all three corresponding sides of two triangles are in same proportion, then they are said to be similar triangles.

Thus, it is named as side, side, side or SSS principle.

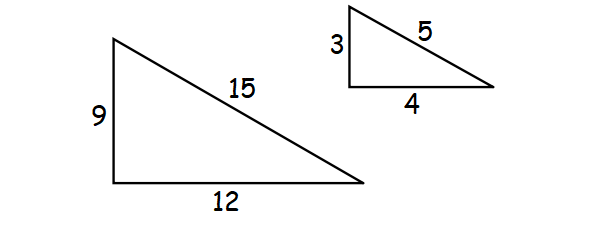
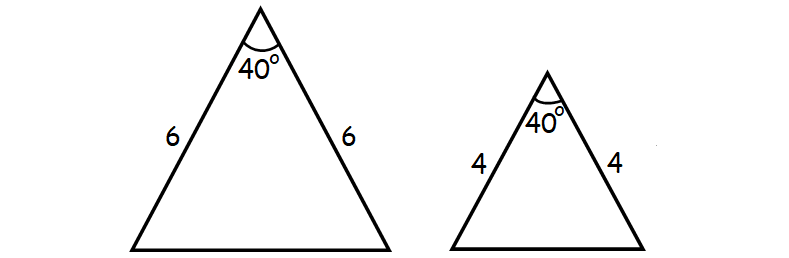
Rule 3 : SAS (Side, Angle, Side)

Two triangles can be proved similar when their two corresponding sides are in same proportion and corresponding angles in between the sides are of same measure.

Therefore, this is called side, angle side or SAS rule.

If you would like to have practice problems on congruent and similar triangles,

please click here

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.