TRIGONOMETRIC FORMULAS

In this section, you will learn different trigonometric formulas.

SOHCAHTOA

sin θ  =  Opposite side/Hypotenuse side

cos θ  =  Adjacent side/Hypotenuse side

tan θ  =  Opposite side/Adjacent side

csc θ  =  Hypotenuse side/Opposite side

sec θ  =  Hypotenuse side/Adjacent side

cot θ  =  Adjacent side/Opposite side

Reciprocal Trigonometric Formulas

sin θ and csc θ are reciprocal to each other

cos θ and sec θ are reciprocal to each other

tan θ and cot θ are reciprocal to each other

Then,

sin θ  =  1/csc θ  and  csc θ  =  1/sin θ

cos θ  =  1/sec θ  and  sec θ  =  1/cos θ

tan θ  =  1/cot θ  and  cot θ  =  1/tan θ

Other Important Trigonometric Formulas 

sin²θ  + cos²θ  =  1

sin²θ  =  1 - cos²θ

cos²θ  =  1 - sin²θ

sec²²θ - tan²θ  =  1

sec²θ  =  1 + tan²θ

tan²θ  =  sec²θ - 1

cosec²θ - cot²θ  =  1

cosec²θ  =  1 + cot²θ

cot²θ  =  cosec²θ - 1

Double Angle Formulas

sin 2A  =  2sin A cos A

cos 2A  =  cos²A - sin²A

tan 2A  =  2tan A/(1 - tan²A)

cos 2A  =  1 - 2sin²A

cos 2A  =  2cos²A - 1

sin 2A  =  2tan A/(1 + tan²A)

cos 2A  =  (1 - tan²A)/(1 + tan²A)

sin²A  =  (1 - cos 2A)/2

cos²A  =  (1 + cos 2A)/2

These identities are applied in both the ways ,left to right and  right to left.

Half Angle Formulas

sin A  =  2sin (A/2) cos (A/2)

cos A  =  cos²(A/2) - sin²(A/2)

 tan A  =  2tan (A/2)/[1 - tan²(A/2)]

cos A  =  1 - 2sin²(A/2)

cos A  =  2cos²(A/2) - 1

 sin A  =  2tan (A/2)/[1 + tan²(A/2)]

cos A  =  [1 - tan²(A/2)]/[1 + tan²(A/2)]

 sin²(A/2)  =  (1 - cos A)/2

cos²(A/2)  =  (1 + cos A)/2

 tan²(A/2)  =  (1 - cos A)/(1 + cos A)

Compound Angles

sin (A + B)  =  sin A cos B + cos A sin B

sin (A + B)  =  sin A cos B + cos A sin B

cos (A + B)  =  cos A cos B - sin A sin B

cos (A - B)  =  cos A cos B + sin A sin B

tan (A + B)  =  (tan A + tan B)/(1 - tan A tan B)

tan (A - B)  =  (tan A - tan B)/(1 + tan A tan B)

Sum to Product Formulas

sin C + sin D  =  2 sin [(C + D)/2] cos [(C - D)/2]

sin C - sin D  =  2 cos [(C + D)/2] Sin [(C - D)/2]

cos C + cos D  =  2 cos [(C + D)/2] Cos [(C - D)/2]

cos C - cos D  =  2 sin [(C + D)/2] Sin [(C - D)/2]

sin3A cos3A tan3A formulas

sin 3A  =  3 sin A - 4 sin³A

cos 3A  =  4 cos³A - 3 cos A

tan 3A  =  (3 tan A - tan³A)/(1 - 3tan²A)

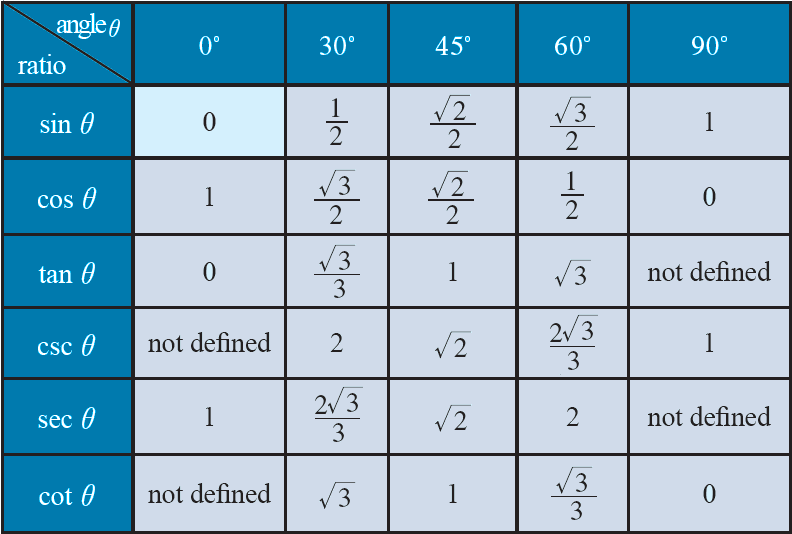
Values of Certain Angles

Solving Word Problems Using Trigonometric Formulas

Step 1 :

Understanding the question and drawing the appropriate diagram are the two most important things to be done in solving word problems in trigonometry.

Step 2 :

If it is possible, we have to split the given information. Because, when we split the given information in to parts, we can understand them easily.

Step 3 :

We have to draw diagram almost for all of the word problems in trigonometry. The diagram we draw for the given information must be correct. Drawing diagram for the given information will give us a clear understanding about the question. 

Step 4 :

Once we understand the given information clearly and correct diagram is drawn, solving word problems in trigonometry would not be a challenging work. 

Step 5 :

After having drawn the appropriate diagram based on the given information, we have to give name for each position of the diagram using English alphabets (it is clearly shown in the word problem given below). Giving name for the positions would be easier for us to identify the parts  of the diagram.

Step 6 :

Now we have to use the appropriate trigonometric formulas (sin, cos and tan) to find the unknown side or angle.

Once the diagram is drawn and we have translated the English Statement (information) given in the question as mathematical equation using trigonometric ratios correctly, 90% of the work will be over. The remaining 10% is just getting the answer. That is solving for the unknown.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.