TRIGONOMETRY PRACTICAL PROBLEMS USING ANGLE OF ELEVATION

Problem 1 :

The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?

Solution :

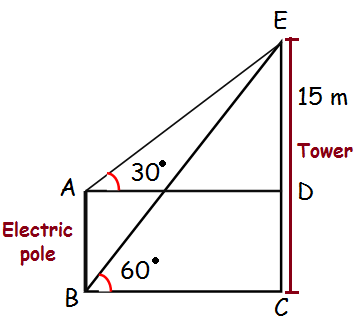
Let DC  =  x, ED  =  15 - x

Height of the electric pole  =  AB  =  DC

AD  =  BC

In triangle AED,

tan θ  =  Opposite side / Adjacent side 

tan 30  =  ED/AD

1/√3  =  (15 - x)/AD

AD  =  (15 - x)√3 ----(1)

In triangle BCE,

tan 60  =  EC/BC

√3  =  15/BC

BC  =  15/√3

BC  =  (15/√3) ⋅ (√3/√3)

BC  =  15√3/3  =  5√3----(2)

(1)  =  (2)

(15 - x)√3  =  5√3

15√3 - x√3  =  5√3

15√3 - 5√3  =  x√3

x  =  10√3/√3

x  =  10

So, the height of the electric pole is 10 m.

Problem 2 :

A vertical pole fixed to the ground is divided in the ratio 1:9 by a mark on it with lower part shorter than the upper part. If the two parts subtend equal angles at a place on the ground, 25 m away from the base of the pole, what is the height of the pole? 

Solution : 

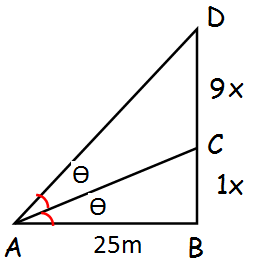
By using angle bisector theorem,

Let the the two parts subtend equal angles at point A such that

CAB  =  DAC  =  θ

BC/DC  =  AB/AD

1/9  =  25/AD

AD  =  25(9)

AD²  =  AB² + BC²

225²  =  25² + (10x)²

100x²  =  225² -  25²

100x²  =  (225 + 25) (225 - 25)

100x²  =  (250) (200)

x²  =  500

x  =  100√5 m

Problem 3 :

A traveler approaches a mountain on highway. He measures the angle of elevation to the peak at each milestone. At two consecutive milestones the angles measured are 4° and 8° . What is the height of the peak if the distance between consecutive milestones is 1 mile. (tan 4° = 0.0699, tan 8° = 0.1405)

Solution :

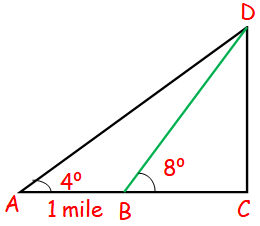
Let BC = x

In triangle BDC,

tan 8  =  DC/BC

  0.1405  =  DC/x

  DC  =  0.1405 x ----(1)

In triangle ADC,

tan 4  =  DC/AC

  0.0699  =  DC/(1 + x)

  DC  =  0.0699(1 + x) ----(2)

(1)  =  (2)

 0.1405 x  =  0.0699(1 + x) 

0.1405 x =  0.0699 + 0.0699 x

(0.1405 - 0.0699)x  =  0.0699

0.0706 x  =  0.0699

x  =  0.0699/0.0706

x  =  699/706

x =  0.99

By applying the value of x in (1), we get 

DC  =  0.1405 (0.99)

DC  =  0.14 mile

So, the height of peak is 0.14 mile.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.