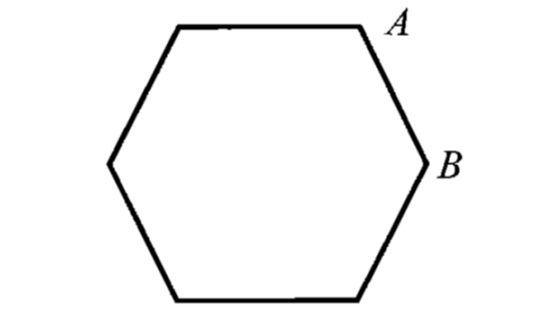
TWO CIRCLES ARE TOUCHING EACH OTHER
Concentric Circles :
Two or more circles having same center is called the concentric circles.
Circles touching each other:
Two circles may touch each other either internally or externally. Let C1, C2 be the centers of the circle and r1, r2 be their radii and P the point of contact.
Case (1) :
The two circles touch externally :
The distance between their centers is equal to the sum of their radii.
C1C2 = r1 + r2
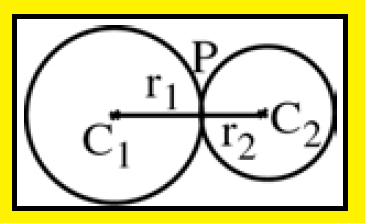
Case (2) :
The two circles touch internally :
The distance between their centers is equal to the difference of their radii.
C1 C2 = C1P − C2P = r1 − r2
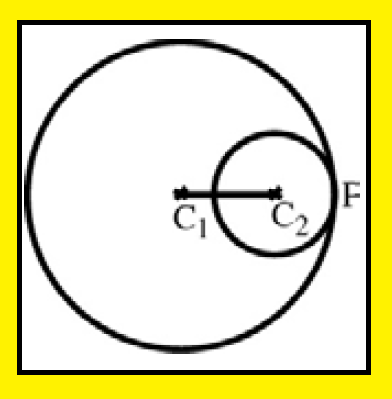
Orthogonal circles :
Two circles are said to be orthogonal if the tangent at their point of intersection are at right angles.
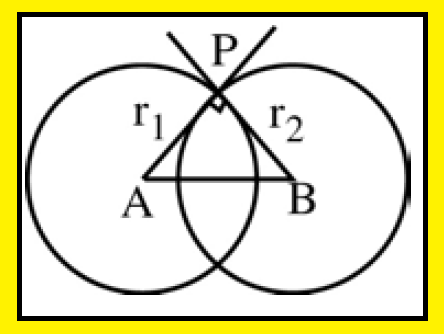
2g1 g2 + 2f1 f2 = c1 + c2
Example 1 :
Find the equation of the circle, which is concentric with the circle
x2 + y2 − 4x − 6y − 9 = 0
and passing through the point (−4, −5).
Solution :
Since the given circle and the required circle are concentric, they will have same center.
x2 + y2 − 4x − 6y − 9 = 0 comparing the equation of general form
x2+y2+2gx+2fy+c = 0
we get,
2g = -4, g = -2
2f = -6, f = -3
Center of given and required circles is (2, 3).
The required circle is passing through the point (-4, -5).
Distance between center and any point on the circle = radius
= √(x2-x1)2 + (y2-y1)2
= √(2+4)2 + (3+5)2
= √(62+82)
= √100
r = 10
Required equation of circle :
(x-h)2+(y-k)2 = r2
(x-2)2+(y-3)2 = 102
By expanding we get,
x2+y2-2x-6y+4+9-100 = 0
x2+y2-2x-6y-87 = 0
Example 2 :
Show that the circles
x2+y2−2x+6y+6 = 0
and
x2+y2−5x+6y+15 = 0
touch each other.
Solution :
By comparing the 1st equation with general form of the circle, we get
2g1 = -2 ==> g1 = -1
2f1 = 6 ==> f1 = 3 and c1 = 6
Center of the first circle (1, -3).
Radius = √g2+f2-c
r1 = √1+9-6
r1 = 2
By comparing the 2nd equation with general form of the circle, we get
2g2 = -5 ==> g2 = -5/2
2f2 = 6 ==> f2 = 3 and c2 = 15
Center of the first circle (5/2, -3).
Radius = √g2+f2-c
r2 = √(25/4)+9-15
r2 = √(25/4)-6
r2 = 1/2
r1 - r2 = 2 - 1/2
r1 - r2 = 3/2-------(1)
Distance between centers :
C1(1, -3) and C2(5/2, -3).
C1C2 = √(x2-x1)2 + (y2-y1)2
C1C2 = √(1-(5/2))2 + (-3+3)2
C1C2 = √(-3/2)2
C1C2 = 3/2 ------(2)
Since the above circles satisfies the condition
C1C2 = r1−r2
the above circles are intersecting each other internally.
Example 3 :
Show that the circle
x2+y2−8x − 6y + 21 = 0
is orthogonal to the circle
x2+y2−2y−15 = 0
Solution :
From 1st equation,
x2+y2−8x − 6y + 21 = 0
2g1 = -8 ==> g1 = -4
2f1 = -6 ==> f1 = -3
c1 = 21
From 2nd equation,
x2+y2−2y−15 = 0
2g2 = 0
2f2 = -2 ==> f2 = -1
c2 = -15
If two circles are intersecting orthogonally, then
2g1 g2 + 2f1 f2 = c1 + c2
2(-4)(0) + 2(-3) (-1) = 21-15
6 = 6
Example 4 :
Circle P has center (-4, -1) and radius 2 units, circle Q has equation x2 + y2 - 2x + 6y + 1 = 0. Show that the circles P and Q do not touch.
Solution :
Calculating radius of circle Q :
x2 + y2 - 2x + 6y + 1 = 0
2g = -2, g = -1
2f = 6, f = 3
Center (-g, -f) ==> (1, -3)
c = 1
radius = √g2 + f2 - c
= √(-1)2 + 32 - 1
= √(1 + 9 - 1)
r = 3
Radius of circle P :
radius = 2
Distance between two centers :
ch
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 9)
Feb 10, 25 06:02 PM
AP Calculus AB Problems with Solutions (Part - 9) -
Digital SAT Math Problems and Solutions (Part - 108)
Feb 10, 25 07:03 AM
Digital SAT Math Problems and Solutions (Part - 108) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Feb 10, 25 07:01 AM
SAT Math Resources (Videos, Concepts, Worksheets and More)