UNION AND INTERSECTION OF SETS PRACTICE

Problem 1  :

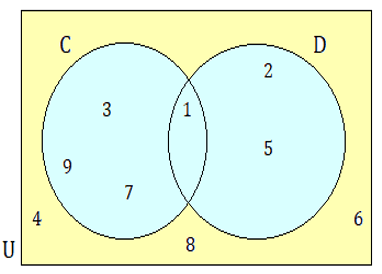
List :

(i)  set C  (ii)  set D  (iii)  set U  (iv)  set CnD   

(v)  set CUD   Solution

Problem 2 :

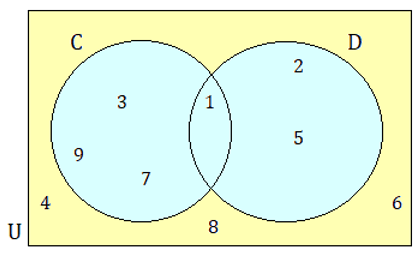
Find :

(i)  n(C)  (ii)  n(D)  (iii)  n(U)  (iv)  n(CnD)  (v)  n(CUD)

Solution

Problem 3 :

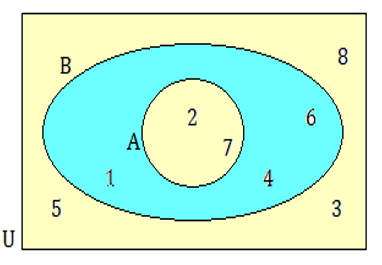
List :

(i)  set A  (ii)  set B  (iii)  set U  (iv)  set AnB  

(v)  set AUB         Solution

Problem 4 :

Find :

(i)  n(A)  (ii) n(B)  (iii) n(U)  (iv) n(AnB)  (v)  n(AUB)

Solution

Problem 5 :

Consider  U  =  {x | x ≤ 12, x Є Z⁺}

A  =  {2, 7, 9, 10, 11} and B  =  {1, 2, 9, 11, 12}

Show these sets on a Venn diagram.

Solution :

Solution

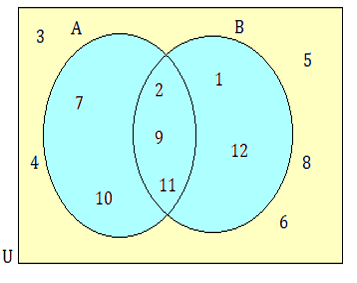
Problem 6 :

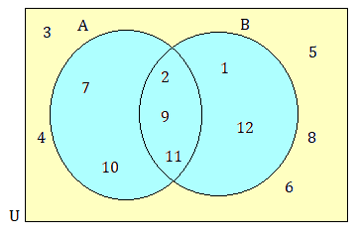
List the elements of :

(i)  AnB  (ii) AUB  (iii)  B’        Solution

Problem 7 :

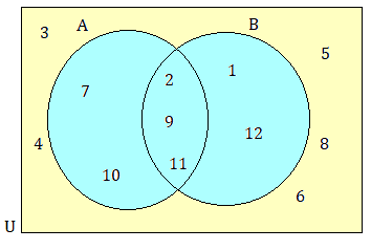
Find :

(i)  n(A)  (ii)  n(B’)  (iii)  n(AnB)  (iv)   n(AUB)

Solution

Problem 8 :

If A is the set of all factors of 36 and B is the set of all factors of 63,

Find : (a)   AnB     (b)   AUB       Solution

Problem 9 :

If X  =  {A, B, D, M, N, P, R, T, Z} and

Y  =  {B, C, M, T, W, Z}

Find :  (a)   XnY     (b)   XUY            Solution

Problem 10 :

If U  =  {x| x ≤ 30, x Є Z⁺}

A  =  {factors of 30} and B  =  {prime numbers ≤ 30}

Find :

(a)  (i)   n (A)   (ii)  n (B)   (iii)  n (A n B)   (iv)  n (A U B)

(b)  Verify that n(AUB)  =  n(A) + n(B) – n(AnB) 

Solution

Answer Key

(1)  (i)  C  =  {1, 3, 7, 9}  (ii)  D  =  {1, 2, 5}

(iii)  U  =  {1, 2, 3, 4, 5, 6, 7, 8, 9}  

(iv)  C n D  =  {1}

(v)  CUD  =  {1, 2, 3, 5, 7, 9}

(2) (i)  n(C)  =  4  (ii)  n(C)  =  3  (iii)  n(U)  =  9

(iv)  n(CnD)  =  1  (v)  n(CUD)  =  6

(3)  (i) A  =  {2, 7}  (ii) B  =  {1, 4, 6, 2, 7}  (iii) U =  {1, 2, 3, 4, 5, 6, 7, 8}  (iv) AnB  =  {2,7}  (v) AUB  =  {1, 2, 4, 6, 7}

(4)  (i)  n(A)  =  2  (ii)  n(B)  =  5  (iii)  n(U)  =  8

(iv)  n(AnB)  =  2  n(AUB)  =  5

(5)  

(6)  (i) AnB  =  {2, 9, 11}

(ii)  AUB  =  {1, 2, 7, 9, 10, 11, 12}

(iii)  B’  =  {3, 4, 5, 6, 7, 8, 10}

(7)  (i)   n(A)  =  5  (ii) n(B')  =  7  (iii)  n(AnB)  =  3

(iv)  n(AUB)  =  7

(8)  (a)  AnB  =  {1, 3, 9}

(b)  AUB  =  {1, 2, 3, 4, 6, 7, 9, 12, 18, 21, 36, 63}

(9)  (a)   XnY  =  {B, M, T, Z}

(b)   XUY  =  {A, B, C, D, M, N, P, R, T, W, Z}

(10)  (i)   n(A)  =  8  (ii)  n(B)  =  10  (iii)  n (AnB)  =  3

(iv)  n (AUB)  =  15

More Word Problems

1)  In a class of 50 students, each of the students passed either in mathematics or in science or in both. 10 students passed in both and 28 passed in science. Find how many students passed in mathematics?

2)  The population of a town is 10000. Out of these 5400 persons read newspaper A and 4700 read newspaper B. 1500 persons read both the newspapers. Find the number of persons who do not read either   of the two papers.

3)   In a school, all the students play either Foot ball or Volley ball or both. 300 students play Foot ball, 270 students play Volley ball and 120 students play both games. Find

(i) the number of students who play Foot ball only

(ii) the number of students who play Volley ball only

(iii) the total number of students in the school

4)  In a School 150 students passed X Standard Examination. 95 students applied for Group I and 82 students applied for Group II in the Higher Secondary course. If 20 students applied neither of the two, how many students applied for both groups?

5)  If the Venn diagram alongside illustrates the number of people in a sporting club who play tennis (T) and hockey (H), determine the number of people:

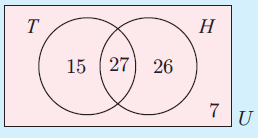
a) in the club

b) who play hockey

c) who play both sports

d) who play neither sport

e) who play at least one sport.

6)  The Venn diagram alongside illustrates the number of students in a particular class who study Chemistry (C) and History (H). Determine the number of students:

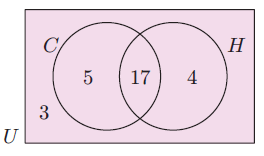
a) in the class

b) who study both subjects

c) who study at least one of the subjects

d) who only study Chemistry.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.