UNION AND INTERSECTION OF SETS

Example 1 :

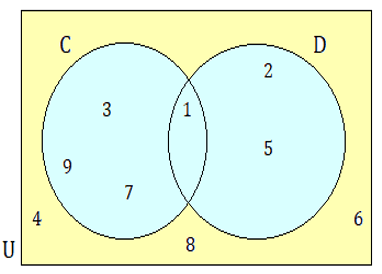
List :

(i)  set C

(ii)  set D

(iii)  set U

(iv)  set CnD 

(v)  set CUD

Solution :

(i)  set C

The elements in set C  =  {1, 3, 7, 9}

(ii)  set D  

The elements in set D  =  {1, 2, 5}

(iii)  set U

The universal set with all the elements in set

U  =  {1, 2, 3, 4, 5, 6, 7, 8, 9}

(iv)  set CnD 

The common elements in sets C and D is

C n D  =  {1}

(v)  set C U D

All the elements in sets C and D is

CUD  =  {1, 2, 3, 5, 7, 9}

Example 2 :

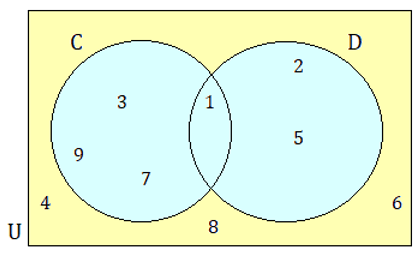
Find :

(i)   n(C)

(ii)  n(D)

(iii)  n(U)

(iv)  n(CnD)

(v)  n(CUD)

Solution :

(i)  n(C)

The number of elements in set C is 4.

So, n(C)  =  4

(ii)  n(D)

The number of elements in set D is 3

So, n(D)  =  3

(iii)  n(U)   

The number of elements in universal set U is 9

n(U)  =  9

(iv)  n (CnD)

The number of common elements in sets C and D is 1.

n(CnD)  =  1

(v)  n (CUD)

The number of all elements in sets C and D is 6.

n(CUD)  =  6

Example 3 :

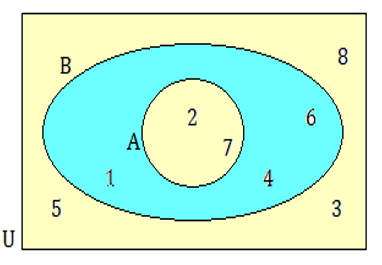
List :

(i)  set A

(ii)  set B

(iii)  set U

(iv)  set AnB

(v)  set AUB

Solution :

(i) A  =  {2, 7}

(ii) B  =  {1, 4, 6, 2, 7}

(iii) U =  {1, 2, 3, 4, 5, 6, 7, 8}

(iv) AnB  =  {2,7}

(v) AUB  =  {1, 2, 4, 6, 7}

Example 4 :

Find :

(i)  n(A)

(ii) n(B)

(iii) n(U)

(iv) n(AnB)

(v)  n(AUB)

Solution :

(i)   n(A)

The number of elements in set A  =  2

(ii)  n(B)

The number of elements in set B  =  5

(iii)  n(U)   

The number of elements in universal set U  =  8

(iv) n(AnB)

The number of common elements in sets A and B is 2

n(AnB)  =  2

(v)  n(AUB)

The number of all elements in sets A and B is 5.

So, n(AUB)  =  5

Example 5 :

Consider  U  =  {x | x ≤ 12, x Є Z⁺}

A  =  {2, 7, 9, 10, 11} and B  =  {1, 2, 9, 11, 12}

Show these sets on a Venn diagram.

Solution :

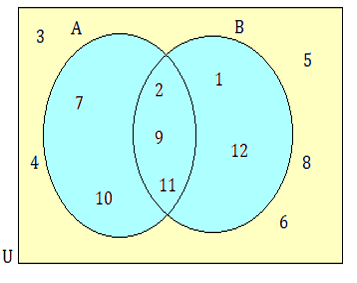
Example 6 :

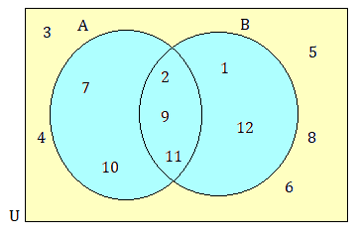
List the elements of :

(i)  AnB

(ii) AUB

(iii)  B’

Solution :

(i) AnB  =  {2, 9, 11}

(ii)  AUB  =  {1, 2, 7, 9, 10, 11, 12}

(iii)  B’

The elements which do not belong to set B is

B’  =  {3, 4, 5, 6, 7, 8, 10}

Example 7 :

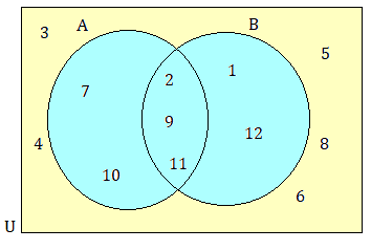
Find :

(i)  n(A)

(ii)  n(B’)

(iii)  n(AnB)

(iv)   n(AUB)

Solution :

(i)   n(A)  =  5

(ii) The number of elements which do not belong to set B is B’  =  7

(iii)  n(AnB)  =  3

(iv)  n(AUB)  =  7

Example 8 :

If A is the set of all factors of 36 and B is the set of all factors of 63,

Find : (a)   AnB     (b)   AUB

Solution :

Given, A is the set of all factors of 36

So, set A  =  {1, 2, 3, 4, 6, 9, 12, 18, 36}

B is the set of all factors of 63

So, set B  =  {1, 3, 7, 9, 21, 63}

(a)  AnB  =  {1, 3, 9}

(b)  AUB  =  {1, 2, 3, 4, 6, 7, 9, 12, 18, 21, 36, 63}

Example 9 :

If X  =  {A, B, D, M, N, P, R, T, Z} and

Y  =  {B, C, M, T, W, Z}

Find :  (a)   XnY     (b)   XUY

Solution :

Given, X  =  {A, B, D, M, N, P, R, T, Z} and

Y  =  {B, C, M, T, W, Z}

(a)   XnY  =  {B, M, T, Z}

(b)   XUY  =  {A, B, C, D, M, N, P, R, T, W, Z}

Example 10 :

If U  =  {x| x ≤ 30, x Є Z⁺}

A  =  {factors of 30} and B  =  {prime numbers ≤ 30}

Find :

(a)  (i)   n (A)   (ii)  n (B)   (iii)  n (A n B)   (iv)  n (A U B)

(b)  Verify that n(AUB)  =  n(A) + n(B) – n(AnB)

Solution :

Given, A  =  {1, 2, 3, 5, 6, 10, 15, 30}

B  =  {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}

(i)   n(A)  =  8

(ii)  n(B)  =  10

(iii)  n (AnB)  =  3

(iv)  n (AUB)  =  15

(b)  n(AUB)  =  n(A) + n(B) – n(AnB)

15  =  8 + 10 – 3

15  =  18-3

15  =  15

Hence it is verified.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.