USING A GRAPH TO ESTIMATE THE SOLUTION OF A SYSTEM

We can use a graph to estimate the solution of a system of equations before solving the system algebraically.

Example 1 :

Estimate the solution by sketching a graph of each linear function. Then solve the system algebraically. Use your estimate to judge the reasonableness of your solution.

x - 4y  =  4

2x - 3y  =  -3

Solution : 

Step 1 :

To sketch the graph of the equations, write them in slope-intercept form.

That is, 

y  =  mx + b  

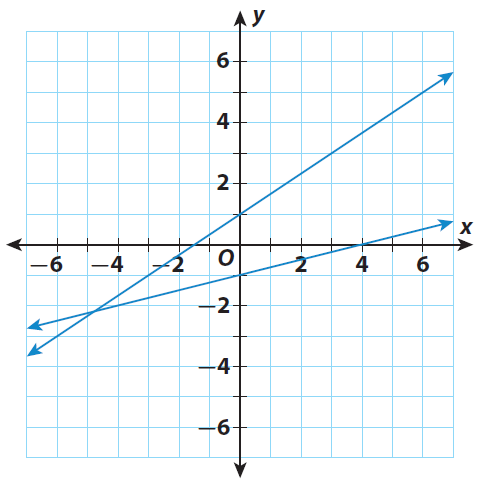
Step 2 :

Find the point of intersection of the lines. The point of intersection is near to the point (-5, -2).

Let us give (-5, -2) as our estimation to the solution of the system. 

Step 3 :

Solve the system algebraically.

Select one of the equation, say x - 4y  =  4.

Solve for the variable x in terms of y. 

Add 4y to both sides. 

(x - 4y) + 4y  =  (4) + 4y

x  =  4 + 4y

Step 4 : 

Substitute the expression for x in the other equation and solve.

2x - 3y  =  -3

2(4 + 4y) - 3y  =  -3

8 + 8y - 3y  =  -3  

Combine the like terms.

8 + 5y  =  -3  

Subtract 8 from both sides. 

5y  =  -11

Divide by 5 on both sides.

5y / 5  =  -11 / 5

y  =  -11/5

Step 5 : 

Substitute the value of y we got above (y = -11/5) into one of the equations and solve for the other variable, y.

x - 4y  =  4

x - 4(-11/5)  =  4

x + 44/5  =  4

Subtract 44/5 from both sides.

x  =  4 - 44/5

x  =  -24/5

Hence, the solution of the system is (-24/5, -11/5).

Step 6 : 

Use the estimate which has been made using the graph to judge the reasonableness of the solution.

-24/5 is close to -5 and -11/5 is close to -2.

So, the solution estimated from the graph (-5, -2) seems reasonable.

Example 2 :

Estimate the solution by sketching a graph of each linear function. Then solve the system algebraically. Use your estimate to judge the reasonableness of your solution.

x + y  =  4

2x - y  =  6

Solution : 

Step 1 :

To sketch the graph of the equations, write them in slope-intercept form.

That is, 

y  =  mx + b  

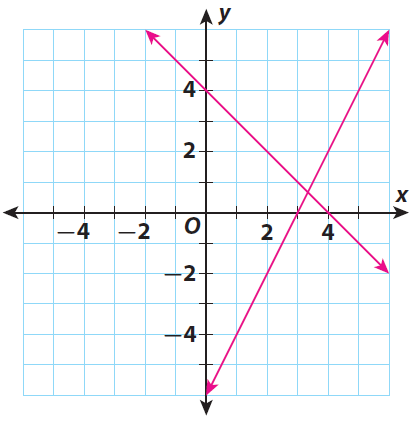
Step 2 :

Find the point of intersection of the lines. The point of intersection is near to the point (3, 1).

Let us give (3, 1) as our estimation to the solution of the system. 

Step 3 :

Solve the system algebraically.

Select one of the equation, say x + y  =  4.

Solve for the variable y in terms of x. 

Subtract x from both sides. 

(x + y) - x  =  (4) - x

y  =  4 - x

Step 4 : 

Substitute the expression for y in the other equation and solve.

2x - y  =  6

2x - (4 - x)  =  6

2x - 4 + x  =  6  

Combine the like terms.

3x - 4  =  6  

Add 4 to both sides. 

3x  =  10

Divide by 3 on both sides.

3x / 3  =  10 / 3

x  =  10/3

Step 5 : 

Substitute the value of x we got above (x = 10/3) into one of the equations and solve for the other variable, y.

x + y  =  4

10/3 + y  =  4

Subtract 10/3 from both sides.

y  =  4 - 10/3

y  =  2/3

Hence, the solution of the system is (10/3, 2/3).

Step 6 : 

Use the estimate which has been made using the graph to judge the reasonableness of the solution.

10/3 is close to 3 and 2/3 is close to 1.

So, the solution estimated from the graph (3, 1) seems reasonable.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.