USING BOXPLOTS TO MAKE INFERENCES

After obtaining a random sample of a  population, we can make inferences about the population. Random samples are usually representative and support valid inferences.

We can use box plots to make inferences from a random sample. 

Box and whisker-plot is the graph used in statistics to represent the central 50% of the values of a data set. 

The picture figure given below clearly illustrates this. 

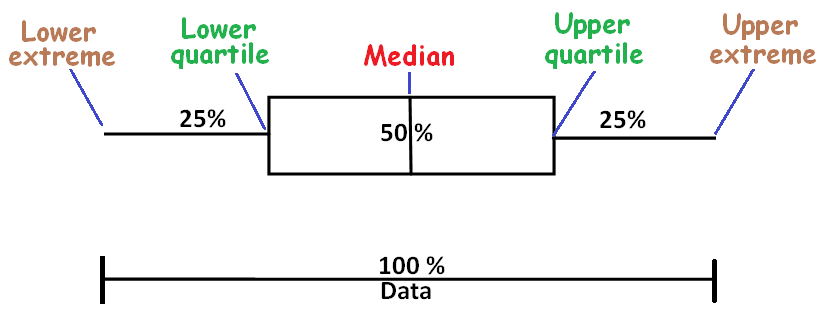
In the above figure, the box spans interquartile range (central 50%).

To draw box and whisker-plot graph for a data set, we have to know lower quartile, upper quartile and median.  

Steps to Construct Box and Whisker Plot

To construct box and whisker-plot for the given data set, we have to do the following steps. 

Step 1 : 

Write the observations of the given data set in ascending order. 

Step 2 : 

Find lower quartile, upper quartile and median using the formulas given below. 

Lower quartile  =  (n + 1)/4

Upper quartile  =  3(n + 1)/4

Median  =  (n + 1)/2

Here, n  =  number of observations in the given data set. 

Step 3 : 

Using lower quartile, upper quartile and median, we have to construct box and whisker-plot as given in the above picture.

Using Boxplots to Make Inferences

The number of pets owned by a random sample of students at Park Middle school is shown below. 

9, 2, 0, 4, 6, 3, 3, 2, 5

(i) Use the data to make a box plot.

Step 1 :

Order the data from least to greatest. Then find the least and greatest values, the median, and the lower and upper quartiles.

Step 2 : 

The lower and upper quartiles can be calculated by finding the medians of each “half” of the number line that includes all the data.

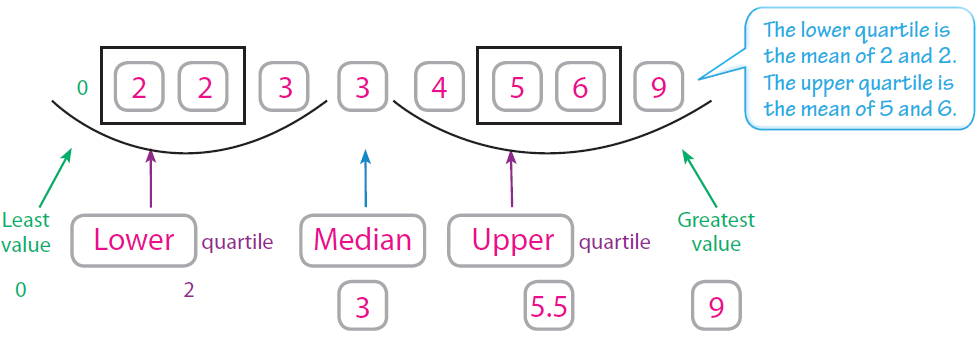
Step 3 : 

Draw a number line that includes all the data values.

Plot a point for each of the values found in Step 1.

Draw a box from the lower to upper quartile. Inside the box, draw a vertical line through the median. Finally, draw the whiskers by connecting the least and greatest values to the box.

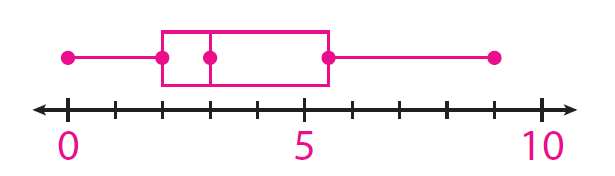
(ii) What is a good measure for the most likely number of pets ?

A good measure for the most likely number of pets is 3.

(iii) How many pets does every student have ?

Almost every student in Parkview has at least 1 pet. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.