USING MATRIX INVERSE TO SOLVE A SYSTEM OF 3 LINEAR EQUATIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
Solve the following linear equation by inversion method
2x + y + z = 5
x + y + z = 4
x - y + 2z = 1
Solution :
First we have to write the given equation in the form
AX = B
Here X
represents the unknown variables. A represent coefficient of the
variables and B represents constants.
|
|
|
To solve this we have to apply the formula X = A⁻¹ B
|
|A| |
|
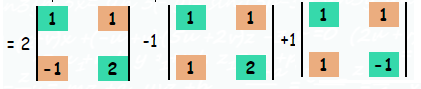
|A| = 2 [2-(-1)] - 1 [2-1] +1 [-1-1]
= 2 [2+1] - 1 [1] +1 [-2]
= 2 [3] - 1 -2
= 6 - 3
= 3
|A| = 3 ≠ 0
Since A is a non singular matrix. A⁻¹ exists.
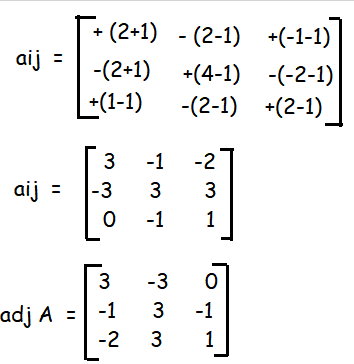
|
A⁻¹ = 1/3 |
|
|
= 1/3 |
|
|
|
x = 15-12+0 x = 3 |
y = -5+12-1 y = 6 |
z = -10+12+1 y = 3 |
x = 3, y = 6 and z = 3
Example 2 :
Solve the following linear equation by inversion method
x + 2y + z = 7
2x - y + 2z = 4
x + y - 2z = -1
Solution :
|
|
|
To solve this we have to apply the formula X = A⁻¹ B
|
|A| |
|
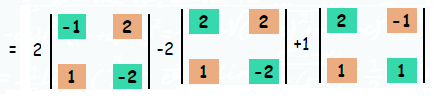
|A| = 2 [2-2] -2[-4-2]+1[2+1]
= 2(0) - 2(-6) + 1(3)
= 0+12+3
|A| = 15 ≠ 0
Since A is a non singular matrix. A⁻¹ exists.
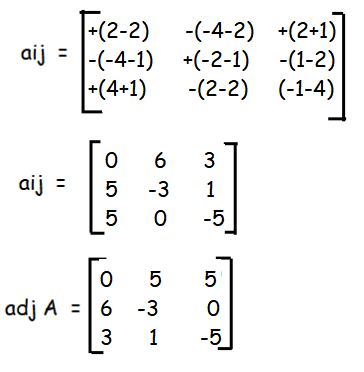
|
= 1/15 |
|
|
|
x = 15/15 x = 1 |
y = 30/15 y = 2 |
z = 30/15 z = 2 |
Example 3 :
Solve the following linear equation by inversion method
2x + y + z = 5
x + y + z = 4
x - y + 2z = 1
Solution :
|
|
|
To solve this we have to apply the formula X = A⁻¹ B
|
|A| |
|
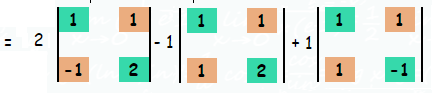
= 2(2+1)+1(2-1)+1(-1-1)
= 2(3)-1-2
= 3
|A| = 3 ≠ 0
Since A is a non singular matrix. A⁻¹ exists
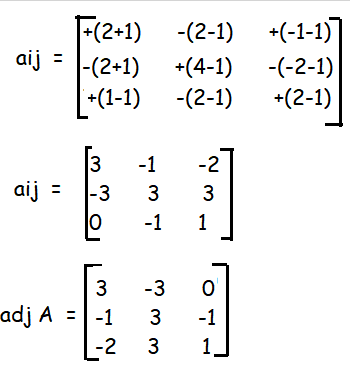
|
= 1/3 |
|
|
|
x = 3/3 x = 1 |
y = 6/3 y = 2 |
z = 30/15 z = 2 |
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 42)
Dec 30, 25 05:52 AM
10 Hard SAT Math Questions (Part - 42) -
10 Hard SAT Math Questions (Part - 38)
Dec 29, 25 04:21 AM
10 Hard SAT Math Questions (Part - 38) -
10 Hard SAT Math Questions (Part - 39)
Dec 28, 25 11:20 PM
10 Hard SAT Math Questions (Part - 39)
