HOW TO CHECK IF THE GIVEN POINTS ARE VERTICES OF RECTANGLE
(i) In a rectangle the length of opposite sides will be equal.
(ii) The rectangle can be divided into two right triangles.
(iii) If the given four vertices satisfies those conditions we can say the given vertices forms a rectangle.
Question 1 :
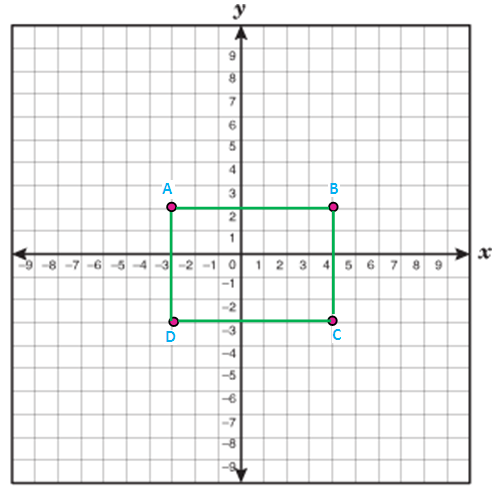
Examine whether the given points
A(-3,2), B(4,2), C (4,-3) and D (-3,-3)
forms a rectangle.
Solution :
Distance Between Two Points (x1, y1) and (x2 , y2)
√(x2 - x1)2 + (y2 - y1)2
Length of AB :
Here x1 = -3, y1 = 2, x2 = 4 and y2 = 2
= √(4-(-3))2 + (2-2)2
= √(4+3)2
= √49
= 7 units
Length of BC :
Here x1 = 4, y1 = 2, x2 = 4 and y2 = -3
= √(4-4)² + (-3-2)²
= √(-5)²
= √25
= 5 units
Length of CD :
Here x1 = 4, y1 = -3, x2 = -3 and y2 = -3
= √(-3-4)² + (-3-(-3))²
= √(-7)² + (-3+3)²
= √49 + 0
= 7 units
Length of DA :
Here x1 = -3, y1 = 2, x2 = -3 and y2 = 2
= √(-3-(-3))2 + (2-(-3))2
= √(-3+3)2 + (2+3)2
= √0 + 52
= 5 units
Length of AC :
Here x1 = -3, y1 = 2, x2 = 4 and y2 = -3
= √(4-(-3))2 + (-3-2)2
= √(4+3)2 + (-5)2
= √72 + 52
= √(49+25)
= √74 units
In triangle ABC,
AC2 = AB2 + BC2
√742 = 72 + 52
74 = 49 + 25
74 = 74
So, the given points are vertices of rectangle.
Question 2 :
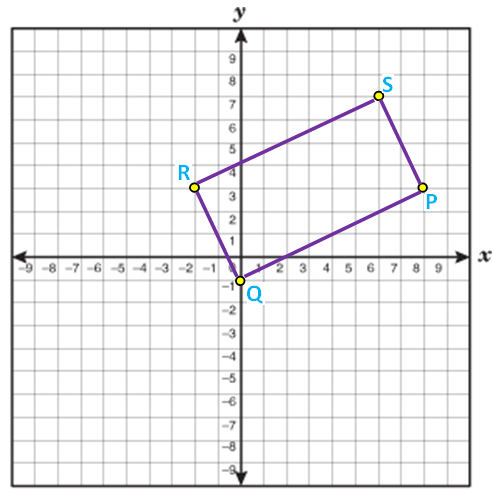
Examine whether the given points
P(8, 3) Q(0, -1) R(-2, 3) and S(6, 7)
forms a rectangle.
Solution :
Length of PQ :
Here x1 = 8, y1 = 3, x2 = 0 and y2 = -1
= √(0-8)2 + (-1-3)2
= √(-8)2 + (-4)2
= √(64+16)
= √80
Length of QR :
Here x1 = 0, y1 = -1, x2 = -2 and y2 = 3
= √(-2-0)2 + (3-(-1))2
= √(-2)² + (3+1)²
= √4 + 16
= √20 units
Length of RS :
Here x1 = -2, y1 = 3, x2 = 6 and y2 = 7
= √(6-(-2))2 + (7-3)2
= √(6+2)2 + 42
= √(64+16)
= √80 units
Length of SP :
Here x1 = 6, y1 = 7, x2 = 8 and y2 = 3
= √(8-6)2 + (3-7)2
= √22 + (-4)2
= √(4+16)
= √20 units
Length of PR :
Here x1 = 0, y1 = -1, x2 = 6 and y2 = 7
= √(6-0)2 + (7-(-1))2
= √36 + 8²
= √36 + 64
= √100 units
In triangle QPS,
QS2 = QP2 + PS2
√1002 = √802 + √202
100 = 80 + 20
100 = 100
So the given vertices forms a rectangle.
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Rational Root Theorem
Feb 06, 25 07:42 PM
Rational Root Theorem or Rational Zero Theorem - Concept - Examples -
How to Find Pythagorean Triplet from One Number
Feb 06, 25 06:10 PM
How to Find Pythagorean Triplet from One Number - Concept - Examples with step by step explanation -
AP Calculus AB Problems with Solutions (Part - 10)
Feb 06, 25 09:46 AM
AP Calculus AB Problems with Solutions (Part - 10)