PROVE THAT THE GIVEN POINTS ARE VERTICES OF RECTANGLE

(i) In a rectangle the length of opposite sides will be equal.

(ii) The rectangle can be divided into two right triangles.

Question 1 :

Examine whether the given points 

A(-2, 7), B (5, 4), C (-1, -10) and D (-8, -7)

forms a rectangle.

Solution :

Distance Between Two Points (x₁, y₁) and (x₂ , y₂)

√(x₂ - x₁)² + (y₂ - y₁)²

Length of AB :

Here x₁ = -2, y₁ = 7, x₂ = 5  and  y₂ = 4

=  √(5-(-2))²+(4-7)²

=  √7²+(-3)²

=  √(49+9)

=  √58 units

Length of BC :

Here x₁ = 5, y₁ = 4, x₂ = -1 and  y₂ = -10

=  √(-1-5)² + (-10-4)²

=  √(-6)² + (-14)²

=  √(36+196)

=  √232 units

Length of CD :

Here x₁ = -1, y₁ = -10, x₂ = -8  and  y₂ = -7

=  √(-8-(-1))² + (-7-(-10))²

=  √(-7)² + 3²

=  √(49+9)

=  √58 units

Length of DA :

Here x₁ = -8, y₁ = -7, x₂ = -2  and  y₂ = 7

=  √(-2-(-8))² + (7-(-7))²

=  √(-2+8)² + (7+7)²

=  √(36+196)

=  √232 units

Length of AC :

Here x₁ = -2, y₁ = 7, x₂ = -1  and  y₂ = -10

=  √(-1-(-2))² + (-10-7)²

=  √(-1+2)² + (-17)²

=  √(1+289)

=  √290 units

In triangle ABC,

AC²  =  AB² + BC²

√290²  =  √58² + √232²

290  =  58 + 232

290  =  290

So, the given points will be the vertices of rectangle.

Question 2 :

Examine whether the given points 

P(-3, 0), Q (1, -2) and R (5, 6) and S (1, 8)

forms a rectangle.

Solution :

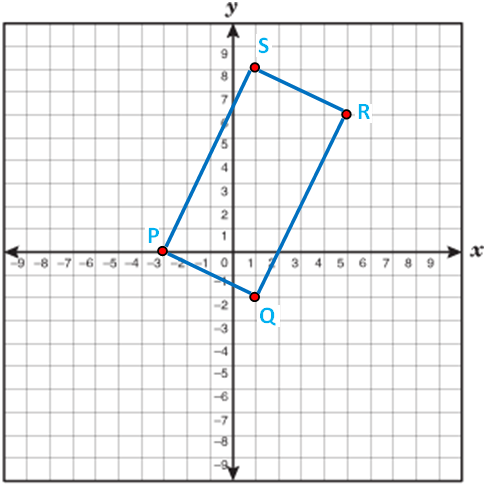
Length of PQ :

Here x₁ = -3, y₁ = 0, x₂ = 1  and  y₂ = -2

=  √(1-(-3))² + (-2-0)²

=  √(1+3)² + (-2)²

=  √4²+(-2)²

=  √(16+4)

=  √20 units

Length of QR :

Here x₁ = 1, y₁ = -2, x₂ = 5 and  y₂ = 6

=  √(5-1)² + (6-(-2))²

=  √4² + (6+2)²

=  √(16 + 64)

=  √80 units

Length of RS :

Here x₁ = 5, y₁ = 6, x₂ = 1 and  y₂ = 8

=  √(1-5)²+(8-6)²

=  √(-4)²+2²

=  √(16+4)

=  √20 units

Length of SP :

Here x₁ = 1, y₁ = 8, x₂ = -3 and  y₂ = 0

=  √(-3-1)² + (0-8)²

=  √(-4)²+(-8)²

=  √(16+64)

=  √80 units

Length of SP :

Here x₁ = 1, y₁ = 8, x₂ = -3 and  y₂ = 0

Here x₁ = 1, y₁ = -2, x₂ = 1  and  y₂ = 8

=    √(1-1)² + (8-(-2))²

=    √(0)² + (8+2)²

=  √0 + 10²

=  √100

=  √100 units

In triangle QRS,

QS²  =  QR² + SR²

(√100)²  =  (√80) ² + (√20)²

100  =  80 + 20

100  =  100

So the given vertices forms a rectangle. 

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.