VERTICES OF SQUARE WORKSHEET

Examine whether the given points forms a square.

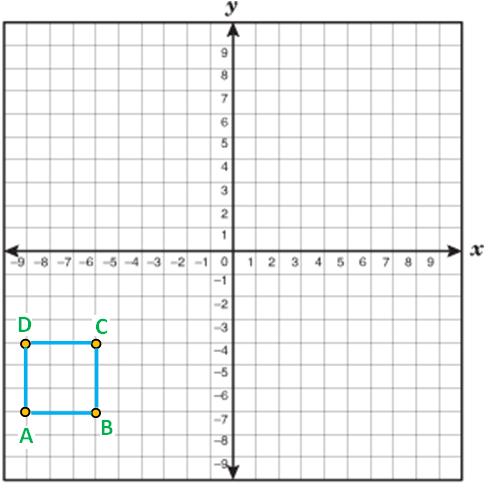
(i)  (-9, -7), B (-6, -7), C (-6, -4) and D (-9, -4)

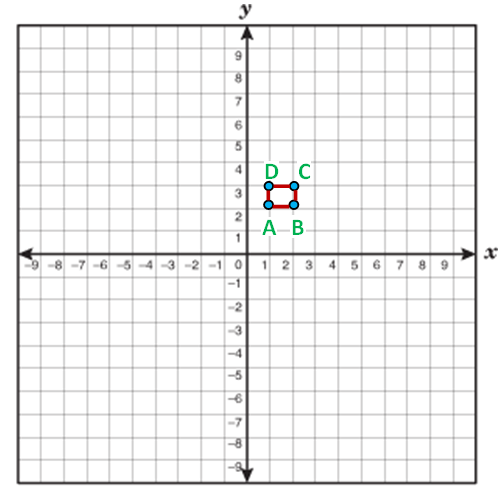
(ii)  A (1, 2) and B (2, 2) and C (2, 3) and D (1, 3)

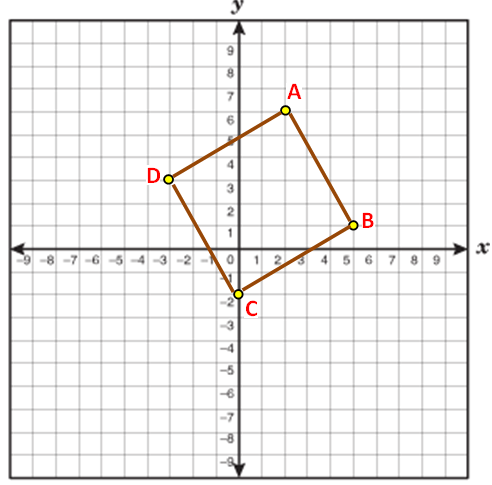
(iii)  A (2, 6), B (5, 1), C (0, -2) and D (-3, 3)

Detailed Solution

Question 1 :

Examine whether the given points 

A (-9, -7), B (-6, -7), C (-6, -4) and D (-9, -4)

form a square.

Solution :

Step 1 :

Step 2 :

Finding the length of all sides.

Distance Between Two Points (x₁, y₁) and (x₂, y₂)

√(x₂ - x₁)² + (y₂ - y₁)²

Length of side AB :

Here x₁ = -9, y₁ = -7, x₂ = -6  and  y₂ = -7

=  √(-6-(-9))² + (-7-(-7))²

=  √(-6+9)² + (-7+7)²

=  √3² + 0²

=  √9

=  3 units ---(1)

Length of side BC :

Here x₁ = -6, y₁ = -7, x₂ = -6  and  y₂ = -4

=  √(-6-(-6))² + (-4-(-7))²

=  √(-6+6)² + (-4+7)²

=  √0² + 3²

=  √9

=  3 units ---(2)

Length of side CD :

Here x₁ = -6, y₁ = -4, x₂ = -9  and  y₂ = -4

=  √(-9-(-6))² + (-4-(-4))²

=  √(-9+6)² + (-4+4)²

=  √(-3)² + 0²

=    √9

=  3 units ---(3)

Length of side DA :

Here x₁ = -9, y₁ = -4, x₂ = -9  and  y₂ = -7

=  √(-9-(-9))² + (-7-(-4))²

=  √(-9+9)² + (-7+4)²

=  √0² + 3²

=  √9

=  3 units ---(4)

(1) = (2) = (3) = (4)

Length of all sides are equal.

Step 3 :

Length of diagonal AC :

Here x₁ = -9, y₁ = -7, x₂ = -6  and  y₂ = -4

=  √(-6-(-9))² + (-4-(-7))²

=  √(-6+9)² + (-4+7)²

=  √3² + 3²

=  √9 + 9

=  √18 units

Length of diagonal BD :

Here x₁ = -6, y₁ = -7, x₂ = -9  and  y₂ = -4

=  √(-9-(-6))² + (-4-(-7))²

=  √(-9+6)² + (-4+7)²

=  √(-3)² + 3²

=  √9 + 9

=  √18 units

Length of diagonal AC  =  Length of diagonal BD

So, the given points are vertices of square.

Question 2 :

Examine whether the given points

A (1, 2), B (2, 2), C (2, 3) and D (1, 3)

forms a square.

Solution :

Step 1 :

Step 2 :

Let the given points are A (1, 2) and B (2, 2) and C (2, 3) and D (1, 3).

Length of side AB :

Here x₁ = 1, y₁ = 2, x₂ = 2  and  y₂ = 2

=  √(2-1)² + (2-2)²

=  √(1)² + (0)²

=  √1 + 0²

=  1 unit ----(1)

Length of side BC :

Here x₁ = 2, y₁ = 2, x₂ = 2  and  y₂ = 3

=  √(2-2)² + (3-2)²

=  √(0)² + (1)²

=  √0² + 1

=  1 unit ----(2)

Length of side CD :

Here x₁ = 2, y₁ = 3, x₂ = 1  and  y₂ = 3

=  √(1-2)² + (3-3)²

=  √(-1)² + (0)²

=  √1 + 0²

=  1 unit ----(3)

Length of side CD :

Here x₁ = 1, y₁ = 3, x₂ = 1  and  y₂ = 2

=  √(1-1)² + (2-3)²

=  √(0)² + (-1)²

=  √0 + 1

=  1 unit  ----(4)

(1) = (2) = (3) = (4)

Step 3 :

Length of diagonal AC :

Here x₁ = 1, y₁ = 2, x₂ = 2  and  y₂ = 3

=  √(2-1)² + (3-2)²

=  √(1)² + 1²

=  √1 + 1

=  √2 units

Length of diagonal BD :

Here x₁ = 2, y₁ = 2, x₂ = 1  and  y₂ = 3

=  √(1-2)² + (3-2)²

=  √(-1)² + (1)

=  √1 + 1

=  √2 units

Length of diagonal AC  =  Length of diagonal BD

So, the given points are vertices of square.

Question 3 :

Examine whether the given points 

A (2, 6), B (5, 1), C (0, -2) and D (-3, 3)

forms a square.

Solution :

Step 1 :

Step 2 :

Finding the length of all sides.

Distance Between Two Points (x₁, y₁) and (x₂, y₂)

√(x₂ - x₁)² + (y₂ - y₁)²

Four points are A (2,6) and B (5,1) and C (0,-2) and D (-3,3)

Length of AB :

Here x₁ = 2, y₁ = 6, x₂ = 5  and  y₂ = 1

=  √(5-2)² + (1-6)²

=  √3²+(-5)²

=  √9+25

=  √34 units  ----(1)

Length of BC :

Here x₁ = 5, y₁ = 1, x₂ = 0  and  y₂ = -2

=  √(0-5)² + (-2-1)²

=  √(-5)² + (-3)2

=  √(25 + 9)

=  √34 units  ----(2)

Length of CD :

Here x₁ = 0, y₁ = -2, x₂ = -3  and  y₂ = 3

=  √(-3-0)² + (3-(-2))²

=  √(-3)² + (3+2)²

=  √9 + 25

=  √34 units  ----(3)

length of DA :

Here x₁ = -3, y₁ = 3, x₂ = 2  and  y₂ = 6

=  √(2-(-3))² + (6-3)²

=  √5² + 3²

=  √25 + 9

=  √34 units  ----(4)

Step 3 :

Length of diagonal AC :

Here x₁ = 2, y₁ = 6, x₂ = 0 and  y₂ = -2

=  √(0-2)² + (-2-6)²

=  √(-2)² + (-8)²

=   √4 + 64

=  √70 units

Length of diagonal BD :

Here x₁ = 5, y₁ = 1, x₂ = -3 and  y₂ = 3

=  √(-3-5)² + (3-1)²

=  √(-8)² + (2)²

=  √64 + 4

=  √70 units

Length of diagonal AC  =  Length of diagonal BD

So, the given points are vertices of square.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.