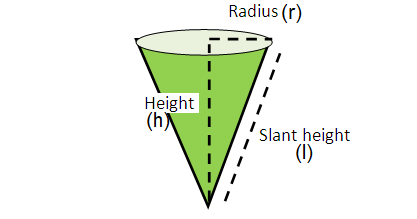
VOLUME OF A CONE WORD PROBLEMS

The formula to find the volume of a cone is given by

V = 1/3 · πr²h cubic units

Problem 1 :

The height and diameter of a cone-shaped storage tank are 9 feet and 14 feet respectively. Find the volume of liquid the tank can hold. Round your answer to the integer, if necessary. Use the approximate of value of π, that is 3.14. 

Solution : 

Step 1 : 

Because the tank is in the shape of cone, we can use the formula of volume of a cone to find volume of water the tank can hold.

Write the formula to find volume of a cone.

V  =  1/3 · πr²h -----(1)

Step 2 : 

To find the volume, we need the radius of the cone. But, the diameter is given, that is 14 ft. So, find the radius. 

r  =  diameter / 2

r  =  14/2

r  =  7

Step 3 : 

Substitute π ≈ 3.14, r = 7 and h = 9 in (1).

V  ≈  1/3 · 3.14 · 7² · 9

Simplify.

V  ≈  1/3 · 3.14 · 49 · 9

V  ≈  461.58

Round it to the nearest integer.

V  ≈  462

So, the volume of the clay is about 462 cubic inches.

Problem 2 :

A silo is shaped like a cone and contains wheat. The radius is 10 feet and the height is 15 feet. If the silo can release wheat from its bottom at the rate of 25 cubic feet per minute, how long would it take for the silo to empty fully ? Round your answer to the nearest minute. Use the approximate of value of π, that is 3.14. 

Solution : 

Step 1 : 

To know how long it would take for the silo to empty fully, first we have to find the volume of wheat in the silo.

Because the silo is in the shape of cone, we can use the formula of volume of a cone to find volume of wheat the tank can hold.

Write the formula to find volume of a cone.

V  =  1/3 · πr²h -----(1)

Step 2 : 

Substitute π ≈ 3.14, r = 10 and h = 15 in (1).

V  ≈  1/3 · 3.14 · 10² · 15

Simplify.

V  ≈  1/3 · 3.14 · 100 · 15

V  ≈  1,570

So, the volume of wheat in the silo is about 1,570 feet. 

Step 3 : 

Silo can release wheat from its bottom at the rate of 25 cubic feet per minute. 

To know how long it would take for the silo to empty 1,570 cubic feet of wheat, divide 1,570 by 25. 

=  1,570 / 25

=  62.8

  ≈  63

So, it would take about 63 minutes for the silo to empty fully.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.