WORD PROBLEMS ON AREA AND CIRCUMFERENCE OF A CIRCLE

Problem 1 :

A cylindrical tank has radius 1.5 m. What is the circumference of its base ?

Solution :

A cylindrical tank has the base which is in the shape of circle.

Circumference of base  =  2πr

radius (r)  =  1.5 m

Circumference of the base  =  2(3.14)(1.5)

=  9.42 m²

So, circumference of the base is 9.42 m².

Problem 2 :

A circular pond has diameter 8 m and needs to be fenced for the protection of children.

a) What length of fencing is required?

b) Fencing comes in 1 m lengths. How many lengths are needed?

c) What is the total cost of the fencing if each length costs $25.00?

Solution :

Diameter of the circular pond  =  8 m, radius  =  4 m

(a)  Length of fencing  =  Circumference of circle

=  2πr 

=  2(3.14) (4) 

=  25.12

So,  length of fencing is 25.12 m.

(b)  Length of each fencing  =  1 m

Number of fencing required  =  26 

(c)  Cost of each fencing  =  $25

Required cost  =  25 (26)

=  $650

So, the required cost is $650.

Problem 3 :

A car wheel has a radius of 35 cm.

a)  What is the circumference of the wheel?

b)  If the wheel rotates 100 000 times, how far does the car travel?

Solution :

Radius of wheel  =  35 cm

Circumference of the wheel  =  2πr

=  2(3.14) (35)

=  219.8

So, circumference of the circle is 220 cm.

(b)  Distance covered in 100 000 times

=  100000(220)

=  22000000 cm

100 cm  =  1 m and 1000 m  =  1 km

=  22000000/100000

=  220 km

So, distance covered by the car is 220 km.

Problem 4 :

A trundle wheel is used for measuring distances. The circumference of the wheel is exactly 1 m. Each time the wheel rotates through one complete turn a click sound is heard and a counter adds a meter to the total. What is the radius of this wheel?

Solution :

Circumference of circle  =  1 m

2πr  =  1

2(3.14) r  =  1

6.28r  =  1

r  =  1/6.28

r  =  0.159 m

100 cm  =  1 m and 1 cm  =  10 mm

r  =  159 mm

So, the required radius is 159 mm.

Problem 5 :

A circular garden plot has circumference 12.65 m. Find its radius in meters, correct to the nearest centimetre.

Solution :

Circumference of circular garden  =  12.65 m

2πr  =  12.65

2(3.14)r  =  12.65

r  =  12.65/6.28

r  =  2.01 m

So, radius of the circular garden is 2.01 m.

Problem 6 :

An irrigation sprinkler sprays water over a field. The radius of the spray is 12.6 m. What area of the field is being watered?

Solution :

Radius of the spray  =  12.6 m

Area of the field is being watered  =  Area of circle

=  πr²

=  3.14(12.6)²

=  3.14(158.76)

=  498.50

So, area of the field is being watered is 498.50 m²

Problem 7 :

The rope connecting a goat to a pole is 8 m long. What area of grass can the goat eat?

Solution :

Length of rope  =  8 m

Area of grass can the goat eat  =  πr²

=  3.14(8)²

=  200.96 

=  201 m²

So, area of grass can the goat eat is 201 m².

Problem 8 :

A circular hoop has a radius of 40 cm. Find the length of tubing needed to make the hoop.

Solution :

Radius of circular hoop  =  40 cm

Length of tubing needed to make a hoop  =  2πr

=  2(3.14)(40)

=  251.2

So, length of tubing needed is 251.2 cm.

Problem 9 :

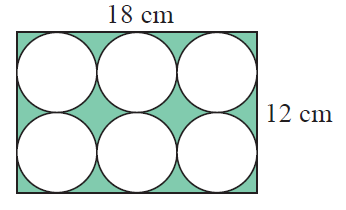
6 identical metal discs are stamped out of an 18 cm by 12 cm sheet of copper as illustrated. What percentage of the copper is wasted

Solution :

Area of 6 stamps  =  6πr²

3(diameter of circle)  =  18

3(2r)  =  18

r  =  18/6

r  =  3 cm

Area  =  6(3.14)(9)

Area of metal discs cut out  =  169.56 cm²

Copper wasted  =  Area of rectangular sheet - Area of metal discs cut out

=  18 x 12 - 169.56

=  216-56.52

=  46.44

=  (46.44/216) ⋅ 100%

=  21.5%

So, copper wasted is 21.5%.

Problem 10 :

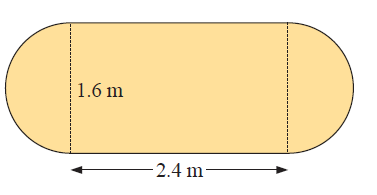
A table-top is shaped as illustrated. A cloth to protect the table-top from stains and heat is cut exactly the same size as the table-top. It is made from fabric 1.6 m wide and costs $18.40 per metre of length.

a) What length of fabric must be purchased?

b) Calculate the cost of the fabric.

c) Find the area of the cloth.

d) Calculate the amount of fabric that is wasted.

Solution :

(a)  Length of fabric to be purchased  =  Side length of one side

=  2.4 + 0.8 + 0.8

=  4 m

So, length of fabric to be purchased is 4 m.

(b)  Cost of fabric  =  $18.40

Cost of fabric purchased  = 18.40(4)

=  $73.60

(c)  Area of cloth 

=  Area of rectangle in the middle + 2(Area of semicircle)

=  2.4(1.6) + 2(πr²/2)

=  3.84 + (3.14)(0.8)²

=  3.84 + 2.0096

=  5.85 m²

d) Amount of fabric wasted  =  (2.4+16) x 1.6 - 2.0096

=  6.4 - 5.85

=  0.55 m²

Problem 11 :

A circular mat has a diameter of 53 centimeters. Lily wants to sew a decorative braid around the mat. How many centimeters of braid does she need? Give your answer to the nearest tenth of a centimeter. Use 3.14 as an approximation of π.

Solution :

Diameter of the circle = 53 centimeters

Circumference of circular mat = πd

= 3.14 (53)

= 166.42 cm

Lliy needs approximately 166.42 cm of decorative braid.

Problem 12 :

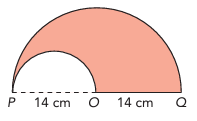
A metalworker cuts out a large semicircle with a diameter of 28 centimeters. Then the metalworker cuts a smaller semicircle out of the larger one and removes it. The diameter of the semicircular piece that is removed is 14 centimeters. Find the distance around the shape after the smaller semicircle is removed. Use 22/7 as an approximation for π.

Solution :

Let R and r be the radius of large semicircle and radius of small semicircle.

R = 14, r = 7  

Length of semicircular arc = length of large semicircle + length of small semicircle + 14

length of large semicircle = (1/2) x 2πR

= π(14)

= 3.14(14)

= 43.96

Approximately 44 cm

length of small semicircle = (1/2) x 2πr

= π(7)

= 3.14(7)

= 21.98

Approximately 22 cm

Length of semicircular arc = 44 + 22 + 14

= 80 cm

The distance around the shape is approximately 80 centimeters.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.