WORD PROBLEMS ON PROBABILITY FOR GRADE 10

Problem 1 :

Two dice are numbered 1,2,3,4,5,6 and 1,1,2,2,3,3 respectively. They are rolled and the sum of the numbers on them is noted. Find the probability of getting each sum from 2 to 9 separately.

Solution :

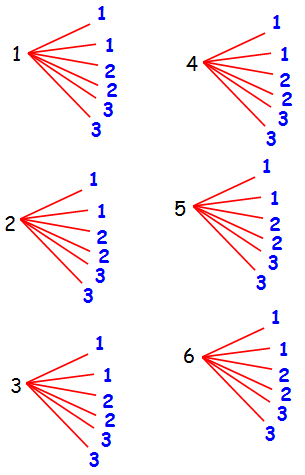
Sample space  =  {(1,1) (2,1) (3,1) (4,1) (5,1) (6,1) (1,1) (2,1) (3,1) (4,1) (5,1) (6,1) (1,2) (2,2) (3,2) (4,2) (5,2) (6,2) (1,2) (2,2) (3,2) (4,2) (5,2) (6,2) (1,3) (2,3) (3,3) (4,3) (5,3)  (6,3) (1,3) (2,3) (3,3) (4,3) (5,3) (6,3) }

n(S)  =  36

Let A, B, C, D, E, F, G, H be the event of getting the sum 2, 3, 4, 5, 6, 7, 8 and 9 respectively.

(i)   Sum 2

A = {(1, 1) (1, 1)}

n(A)  =  2

P(A)  =  2/36

(ii) Sum 3

B = { (2, 1) (2, 1) (1, 2) (1,2) }

n(B)  =  4

P(B)  =  4/36

(iii) Sum 4

C = { (3,1) (3,1) (2,2) (2,2) (1,3) (1,3) }

n(C)  =  6

P(C)  =  6/36

(iv) Sum 5

D = {(4,1) (4,1) (3,2)(3,2) (2,3) (2,3)}

n(C)  =  6

P(C)  =  6/36

(v) Sum 6

E = {(5, 1) (5, 1) (4, 2) (4, 2) (3, 3) (3, 3) }

n(E)  =  6

P(E)  =  6/36

(vi) Sum 7

F = {(6, 1) (6, 1) (5, 2) (5, 2) (4, 3) (4, 3) }

n(F)  =  6

P(F)  =  6/36

(vii) Sum 8

G = {(6,2) (6,2) (5,3) (5,3)} 

n(G)  =  4

P(G)  =  4/36

(viii) Sum 9

H = { (6,3)(6,3)} 

n(H)  =  2

P(H)  =  2/36

Problem 2 :

A bag contains 5 red balls, 6 white balls, 7 green balls, 8 black balls. One ball is drawn at random from the bag. Find the probability that the ball drawn is (i) white (ii) black or red (iii) not white (iv) neither white nor black

Solution : 

Total number of balls  =  5 red + 6 white + 7 green + 8 black

n(S)  =  26

(i)  Let "A" be the event of getting white ball

n(A)  =  6

P(A)  =  n(A)/n(S)

P(A)  =  6/26

P(A)  =  3/13

(ii) black or red

Let "B" be the event of getting black or red ball

n(B)  =  5 + 8

n(B)  =  13

P(B)  =  13/36

P(B)  =  1/2

(iii) not white 

P(A bar)  =  1 - P(A)

  =  1 - (3/13)

  =  (13 - 3)/13

P(A bar)  =  10/13

(iv) neither white nor black

Let "C" be the event of getting neither white nor black

C  =  5 red + 7 green

n(C)  =  12

P(C)  =  12/26

P(C)  =  6/13

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.