WORKSHEET ON PROFIT AND LOSS PERCENTAGE

Problem 1 :

Cindy bought 50 pens for $100. She then sold each pen for $2.50. Find the profit or loss percentage. 

Problem 2 :

Jacob purchased a house for $49,000. He spent $6000 for repair and $5,000 for air-conditioning. If he had sold the house $58,000, find the gain or loss percentage in this transaction. (If it is needed, round your answer to the nearest hundredths)

Problem 3 :

Goods are purchased for $1500. If one fifth of the goods sold at a profit of 5% and the remaining four-fifth of the goods at a profit of 10%, find the net profit percentage.   

Problem 4 :

A trader bought a product for $200. If marks his goods 20% above the cost price and gives a discount of 10% for cash, find his profit percentage.

Problem 5 :

A person wants to get 20% profit after selling his object at 20% discount. Find the required percentage increase in marked price. 

Solutions

Problem 1 :

Cindy bought 50 pens for $100. She then sold each pen for $2.50. Find the profit or loss percentage. 

Solution :

Cost price of 50 pens  =  $100

Cost price of 1 pen  =  100/50  =  $2

Selling price of 1 pen  =  $2.50

Because the selling price of 1 pen is more than cost price of 1 pen, there is profit. 

Finding Profit :

Profit  =  Selling price - Cost price

Profit  =  2.50 - 2

Profit  =  0.50

Finding Profit Percentage :

Profit %  =  (Profit/Cost price) ⋅ 100 %

Profit %  =  (0.50/2) ⋅ 100 %

Profit %  =  25 %

Problem 2 :

Jacob purchased a house for $49,000. He spent $6000 for repair and $5,000 for air-conditioning. If he had sold the house $58,000, find the gain or loss percentage in this transaction. (If it is needed, round your answer to the nearest hundredths)    

Solution :

Total amount spent on the house is

=  49,000 + 6,000 + 5,000

=  60,000

This is the cost price of the house ($60,000). 

Selling price of the house  =  $58,000

Because the selling price of the house is less than the cost price, there is loss. 

Finding Loss :

Loss  =  Cost price - Selling price

Loss  =  60,000 - 58,000

Loss  =  2,000

Finding Loss Percentage :

Loss %  =  (Loss/Cost price) ⋅ 100 %

Loss %  =  (2000/60000) ⋅ 100 %

Loss %  =  3.33 %

Problem 3 :

Goods are purchased for $1500. If one fifth of the goods sold at a profit of 5% and the remaining four-fifth of the goods at a profit of 10%, find the net profit percentage.   

Solution :

Cost price of one-fifth of the goods is

=  1/5 ⋅ 1500

=  300

Selling price of one-fifth of the goods (at 5% profit) is 

=  (100 + 5)% of 300

=  105% of 300

=  1.05 ⋅ 300

=  315

Cost price of remaining four-fifth of the goods is

=  4/5 ⋅ 1500

=  1,200

Selling price of the remaining four-fifth of the goods (at 10% profit) is 

=  (100 + 10)% of 1200

=  110% of 1200

=  1.10 ⋅ 1200

=  1,320

Selling price of the total goods

=  315 + 1,320

=  1,635

Finding Net Profit :

Net profit  =  S.P of total goods - C.P of total goods

Net Profit  =  1635 - 1500

Net Profit  =  135

Finding Net Profit Percentage :

Net profit %  =  (Net profit/Cost price) ⋅ 100 %

Net profit %  =  (135/1500) ⋅ 100 %

Net profit %  =  9 %

Problem 4 :

A trader bought a product for $200. If marks his goods 20% above the cost price and gives a discount of 10% for cash, find his profit percentage

Solution :

Cost price of the product  =  $100 

Marked price (20% above the cost price) is

=  (100 + 20) % of 200

=  120% of 200

=  1.2 ⋅ 200

=  240

Selling price price is the price which is after 20% discount from the marked price. 

So, the selling price is 

=  (100 - 10) % of Marked price

=  90% of 240

=  0.9 ⋅ 240

=  216

Finding Profit :

Profit  =  Selling price - Cost price

Profit  =  216 - 200

Profit  =  16

Finding Profit Percentage :

Profit %  =  (Profit/Cost price) ⋅ 100 %

Profit %  =  (16/200) ⋅ 100 %

Profit %  =  8 %

Problem 5 :

A person wants to get 20% profit after selling his object at 20% discount. Find the required percentage increase in marked price. 

Solution :

Let the cost price be $100. 

Then, the selling price (at 20% profit) is

=  (100 + 20)% of 100

=  120% of 100

=  1.2 ⋅ 100

=  120

Selling price price is the price which is after 20% discount from the marked price. 

It has been illustrated in the picture given below. 

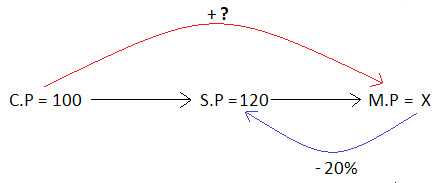
From the above picture, we get 

Selling price  =  (100 - 20)% of Mmarked price

120  =  80% of x

120  =  0.8 ⋅ x

Divide both sides by 0.8

120/0.8  =  x

1200/8  =  x

150  =  x

So, the marked price is $150. 

Here,

Cost price  =  $100

Marked Price  =  $150

Hence, the required percentage increase is 50%

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.