WRITE THE COMPLEX NUMBER IN POLAR FORM

Polar form or trigonometric form :

The complex number a + bi is written in polar form as,

z  =  r(cos θ + i sin θ)

(where a  =  r cos θ, and b  =  r sin θ)

The value of r is called the modulus of a complex number z. i.e, r  =  |z|

To find the r, we use the formula r  =  √(a² + b²).

The angle θ is called the argument of the complex number z. i.e, θ  =  arg(z). 

To find the arg(z), we will use α  =  tan^-1|b/a|.

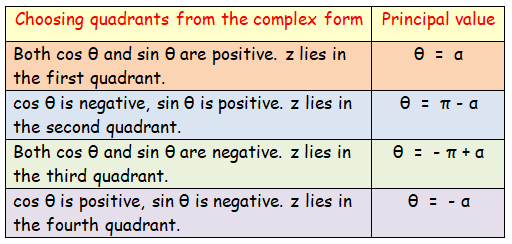
To find the principal value θ of a complex number, we may use the following methods.

Find the trigonometric form of the complex number where the argument satisfies 0 ≤ θ < 2π :

Example 1 :

3i

Solution :

Given, z  =  0 + 3i

The polar form of the complex number z is

r(cos θ + i sin θ)

0 + 3i  =  r(cos θ + i sin θ) -----(1)

Since the complex number 0 + 3i is positive, z lies in the first quadrant.

So, the principal value θ  =  π/2

By applying the value of r and θ in equation (1), we get

0 + 3i  =  3(cos π/2 + i sin π/2)

So, the polar form of z is 3(cos π/2 + i sin π/2)

Example 2 :

-2i

Solution :

Given, z  =  0 - 2i

0 - 2i  =  r(cos θ + i sin θ) -----(1)

Since the complex number 0 - 2i is positive and negative, z lies in the fourth quadrant.

So, the principal value θ  =  - π/2

By applying the value of r and θ in equation (1), we get

0 – 2i  =  2(cos (-π/2) + i sin (-π/2))

So, the polar form of z is 2(cos (-π/2) + i sin (-π/2))

Example 3 :

2 + 2i

Solution :

Given, z  =  2 + 2i

2 + 2i  =  r(cos θ + i sin θ) -----(1)

Since the complex number 2 + 2i is positive, z lies in the first quadrant.

So, the principal value θ  =  π/4

By applying the value of r and θ in equation (1), we get

2 + 2i  =  2√2(cos π/4 + i sin π/4)

So, the polar form of the complex number z is

2√2(cos π/4 + i sin π/4)

Example 4 :

√3 + i

Solution :

Given, z  =  √3 + i

√3 + i  =  r(cos θ + i sin θ) -----(1)

Since the complex number √3 + i has a positive, z lies in the first quadrant.

So, the principal value θ  =  π/6

By applying the value of r and θ in equation (1), we get

√3 + i  =  2(cos π/6 + i sin π/6)

So, the polar form of z is 2(cos π/6 + i sin π/6)

Example 5 :

-2 + 2i√3

Solution :

Given, z  =  -2 + 2i√3

-2 + 2i√3  =  r(cos θ + i sin θ) -----(1)

Since the complex number -2 + 2i√3 is negative and positive, z lies in the second quadrant.

So, the principal value θ  =  π - π/3

θ  =  2π/3

By applying the value of r and θ in equation (1), we get

-2 + 2i√3  =  4(cos 2π/3 + i sin 2π/3)

So, the polar form of z is 4(cos 2π/3 + i sin 2π/3)

Example 6 :

3 - 3i

Solution :

Given, z  =  3 - 3i

3 – 3i  =  r(cos θ + i sin θ) -----(1)

Since the complex number 3 - 3i has a positive and negative, z lies in the fourth quadrant.

So, the principal value θ  =  – π/4

By applying the value of r and θ in equation (1), we get

3 - 3i  =  4(cos (-π/4) + i sin (-π/4))

So, the polar form of z is 4(cos (-π/4) + i sin (-π/4))

Related pages

• Product of complex numbers in polar form
  
• Division of complex numbers in polar form

Apart from the stuff given above,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.