WRITE THE GIVEN PRODUCT EXPRESSION AS WHOLE NUMBER

Exponents are used to avoid the repetition of writing the same numerical values many times.

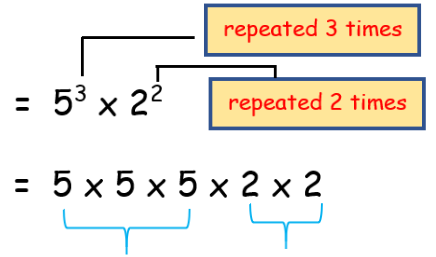
Example 1  :

2 × 3 × 5

Solution :

=  2 × 3 × 5

By converting it as whole number, we get

=  6 × 5

=  30

So, the whole number is 30.

Example 2 :

2² × 5

Solution :

=  2² × 5

2² written as 2 × 2

By converting it as whole number, we get

=  2 × 2 × 5

=  20

So, the whole number is 20.

Example 3 :

2³ × 7

Solution :

=  2³ × 7

2³ written as 2 × 2 × 2

By converting it as whole number, we get

=  2 × 2 × 2 × 7

=  56

So, the whole number is 56.

Example 4 :

2 × 3³ × 5

Solution :

Given,

2 × 3³ × 5

3³ written as 3 × 3 × 3

By converting it as whole number, we get

=  2 × 3 × 3 × 3 × 5

=  270

So, the whole number is 270.

Example 5 :

2² × 3² × 11

Solution :

=  2² × 3² × 11

2² and 3² written as 2 × 2 and 3 × 3

By converting it as whole number, we get

=  2 × 2 × 3 × 3 × 11

=  396

So, the whole number is 396.

Example 6 :

2³ × 5² × 11²

Solution :

=  2³ × 3² × 11²

2³  =  2 × 2 × 2

3²  =  3 × 3

11²  =  11 × 11

By converting it as whole number, we get

=  2 × 2 × 2 × 3 × 3 × 11 × 11

=  8712

So, the whole number is 8712.

Example 6 :

1⁰ + 2⁰ + 3⁰ is equal to 

a) 0     b)  1     c) 3    d) 6

Solution :

1⁰ + 2⁰ + 3⁰

Anything to the power is 1.

= 1 + 1 + 1

= 3

Example 7 :

The value of (10²² + 10²⁰) / 10²⁰ is equal to 

a) 10     b)  10⁴²     c) 101    d) 10²²

Solution :

= (10²² + 10²⁰) / 10²⁰ 

= 10²⁰(10² + 1)/10²⁰

Cancelling the common factors in both numerator and denominator, we get

= (10² + 1)

= 100 + 1

= 101

Example 8 :

If

2¹⁹⁹⁸ – 2¹⁹⁹⁷ – 2¹⁹⁹⁶ + 2¹⁹⁹⁵ = K.2¹⁹⁹⁵

 then the value of K is

(a) 1    (b) 2    (c) 3    (d)  4

Solution :

2¹⁹⁹⁸ – 2¹⁹⁹⁷ – 2¹⁹⁹⁶ + 2¹⁹⁹⁵ = K.2¹⁹⁹⁵

Factoring 2¹⁹⁹⁵, we get

2¹⁹⁹⁵(2³ - 2² - 2 + 1) = K.2¹⁹⁹⁵

Cancelling 2¹⁹⁹⁵, we get

(2³ - 2² - 2 + 1) = K

8 - 4 - 2 + 1 = k

8 - 6 = k

k = 2

Example 9 :

Which of the following is equal to 1?

(a) 2⁰ + 3⁰ + 4⁰          (b) 2⁰ × 3⁰ × 4⁰

(c) (3⁰ – 2⁰) × 4⁰      (d)  (3⁰ – 2⁰) × (3⁰ + 2⁰)

Solution :

Let us evaluate the options one by one.

Option a :

= 2⁰ + 3⁰ + 4⁰

Anything to the power 0 is 1.

= 1 + 1 + 1

= 3

Option b :

2⁰ × 3⁰ × 4⁰

= 1 x 1 x 1

= 1

So, option b is correct.

State the following statements are true or false.

Example 10 :

4⁹ is greater than 16³

Solution :

To compare these two, we have to make the power or base as same. After that the comparison can be done simply.

4⁹ = (2 x 2)⁹

= (2²)⁹

= 2¹⁸ ------(1)

16³ = (2 x 2 x 2 x 2)³

= (2⁴)³

= 2¹² ------(2)

After comparing (1) and (2), we get

2¹⁸ > 2¹²

So, the given is true.

Example 11 :

8 × 10⁶ + 2 × 10⁴ + 5 × 10² + 9 × 10⁰ = 8020509

Solution :

8 × 10⁶ + 2 × 10⁴ + 5 × 10² + 9 × 10⁰

= 8 x 1000000 + 2 x 10000 + 5 x 100 + 9 x 1

= 8000000 + 20000 + 500 + 9

= 8020509

So, the given expression is true.

Example 12 :

Arrange is ascending order

2²⁺³, (2²)³, 2³x 2, 3⁵/3², 3²x 3⁰, 2³x 5²

Solution :

2²⁺³, (2²)³, 2³x 2, 3⁵/3², 3²x 3⁰, 2³x 5²

• 2²⁺³ = 2⁵ ==> 32
• (2²)³ = 2⁶ ==> 64
• 2³x 2 = 8 x 2 ==> 16
• 3⁵/3² = 3³ ==> 27
• 3²x 3⁰ = 9 x 1 ==> 9
• 2³x 5² = 8 x 25 ==>  200

Arranging from least to greatest,

9, 16, 27, 32, 64, 200

3²x 3⁰, 2³x 2, 3⁵/3², 2²⁺³, (2²)³, 2³x 5²

Example 13 :

Arrange is descending order

2⁵, 3³, 2³x 2, (3³)², 3⁵, 4⁰, 2³x 8

Solution :

2⁵, 3³, 2³x 2, (3³)², 3⁵, 4⁰, 2³x 8

• 2⁵ ==> 64
• 3³ ==> 27
• 2³x 2 = 8 x 2 ==> 16
• (3³)² = 3⁴ ==> 81
• 3⁵ ==> 243
• 4⁰ ==> 1
•  2³x 8 = 8 x 8 ==> 64

Arranging from greatest to least.

243, 81, 64, 27, 16, 1

3⁵ , (3³)²,  2³x 8, 3³, 2³x 2, 4⁰

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.