WRITING POLYNOMIALS IN STANDARD FORM

Question 1 :

Rewrite each the following polynomials in standard form.

(i)  x - 9 + √7x³ + 6x²

Solution :

Standard form of the given polynomial is  

√7x³ + 6x² + x - 9

(ii)   √2x² - (7/2)x⁴ + x - 5x³

Solution :

Standard form of the given polynomial is  

- (7/2)x⁴ - 5x³ + √2x² + x

(iii)   7x³ - (6/5)x² + 4x - 1

Solution :

The given polynomial is already in standard form.

(iv)   y² - √5y³ - 11 - (7/3)y + 9y⁴

Solution :

Standard form of the given polynomial is

=  9y⁴- √5y³ + y² - (7/3)y - 11

Question 2 :

Add the following polynomials and write the resultant polynomials in standard form. 

(i)  p(x)  =  6x² - 7x + 2 and q(x)  =  6x³ - 7x + 15

Solution :

p(x) + q(x)  =  (6x² - 7x + 2) + (6x³ - 7x + 15) 

=  6x² - 7x + 2 + 6x³ - 7x + 15

=  6x³ + 6x² - 7x - 7x + 2 + 15

=  6x³ + 6x² - 14x + 17

(ii)  h(x)  =  7x³ - 6x + 1, f(x)  =  7x² + 17x - 9

Solution :

h(x) + f(x)  =  (7x³ - 6x + 1) + (7x² + 17x - 9)

=  7x³ + 7x²- 6x + 17x + 1 - 9

=  7x³ + 7x² + 11x - 8

(iii)  f(x)  =  16x⁴ - 5x² + 9, g(x)  =  -6x³ + 7x - 15

Solution :

f(x) + g(x)  =  (16x⁴ - 5x² + 9) + (-6x³ + 7x - 15)

=  16x⁴- 6x³  - 5x² + 7x + 9 - 15

=  16x⁴- 6x³  - 5x² + 7x  - 6

Question 3 :

If m = 4n + 5 and p = 3n + 6, which of the following expresses n in terms of m and p?

(A) m + 2p - 3     (B) m - p + 1      (C) 3m - 2p + 4

(D) 4m + p + 1       (E) 2m - 5p

Solution :

m = 4n + 5 and p = 3n + 6

Writing 3n as 4n - 1n and 6 as 5 + 1, 

p = 4n - n + 5 + 1

p = (4n + 5) - n + 1

p = m - n + 1

So, option B is correct.

Question 4 :

Which expression is equivalent to

(x² + 11)² + (x + 5)(x - 5) ?

A)  x⁴ + 23x² - 14          B)  x⁴ + 23x² + 96

C)  x⁴ + 12x² + 121          D)  x⁴ + x² + 146

Solution :

= (x² + 11)² + (x + 5)(x - 5)

= x⁴ + 2x² (11) + 11² + x² - 5²

= x⁴ + 22x² + 121 + x² - 25

= x⁴ + 23x² + 96

So, option B is correct.

Question 5 :

x² y - 3y² + 5xy² - (-x² y + 3xy² - 3y²)

Solution :

= x² y - 3y² + 5xy² - (-x² y + 3xy² - 3y²)

= x² y - 3y² + 5xy² + x² y - 3xy² + 3y²

= x² y + x² y - 3y² + 3y² + 5xy² - 3xy²

= 2x² y + 2xy²

Question 6 :

If x + y = 10, what is the sum of (x + y)²  and (x + y) ?

A)  90     B) 100    C)  110     D)  200      E)  210

Solution :

Given that, x + y = 10

= (x + y)² + (x + y)

= 10² + 10

= 100 + 10

= 110

So, the answer is option C.

Question 7 :

(x + 5) + (2x - 3)

Which of the following in equivalent to the given expression.

A)  3x - 2     B)  3x + 2      C)  3x - 8     D)  3x + 8

Solution :

= (x + 5) + (2x - 3)

= x + 5 + 2x - 3

= x + 2x + 5 - 3

= 3x + 2

So, option B is correct.

Question 8 :

What is the distance around the rectangle if the length is 3x² + 6x – 10 and the width is 3x + 5?

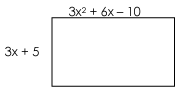
Solution :

Length of the rectangle = 3x² + 6x – 10

Width of the rectangle = 3 x + 5

Perimeter of the rectangle = 2(length + width)

= 2 (3x² + 6x – 10 + 3x + 5)

= 2 (3x² + 6x + 3x – 10 + 5)

= 2 (3x² + 9x – 5)

Distributing 2, we get

= 6x² + 18x – 10

So, the required perimeter of the rectangle is 

6x² + 18x – 10

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.